题目内容
4.已知数列{an}是等差数列,且a4=a2+4,a3=6,则数列{an}的通项公式是2n,数列$\left\{{{2^{a_n}}}\right\}$的前n项和Tn为$\frac{4}{3}({4}^{n}-1)$.分析 设等差数列{an}的公差为d,由于a4=a2+4,a3=6,可得$\left\{\begin{array}{l}{{a}_{1}+3d={a}_{1}+d+4}\\{{a}_{1}+2d=6}\end{array}\right.$,解得a1,d.可得an,由于${2}^{{a}_{n}}={2}^{2n}$=4n.利用等比数列的前n项和公式可得Tn.
解答 解:设等差数列{an}的公差为d,∵a4=a2+4,a3=6,
∴$\left\{\begin{array}{l}{{a}_{1}+3d={a}_{1}+d+4}\\{{a}_{1}+2d=6}\end{array}\right.$,解得a1=d=2.
∴an=2+2(n-2)=2n,
${2}^{{a}_{n}}={2}^{2n}$=4n.
∴Tn=$\frac{4({4}^{n}-1)}{4-1}$,
化为${{T}_n}=\frac{4}{3}({{4^n}-1})$.
故答案分别为:2n;$\frac{4}{3}({4}^{n}-1)$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.已知数列{an}满足a1=2,an+1=$\frac{{1+{a_n}}}{{1-{a_n}}}$,则a15等于( )
| A. | 2 | B. | -3 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{3}$ |
9.下面关于算法的说法正确的是( )
| A. | 秦九韶算法是求两个数的最大公约数的方法 | |
| B. | 更相减损术是求多项式的值的方法 | |
| C. | 割圆术是采用正多边形面积逐渐逼近圆面积的算法计算圆周率π | |
| D. | 以上结论皆错 |
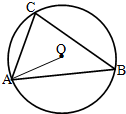 如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.
如图所示,在△ABC中,AB=4,AC=2,若O为△ABC的外心.
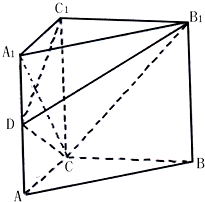 某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.
某家居装饰设计的形状是如图所示的直三棱柱ABC-A1B1C1,其中,∠ACB=90°,BCC1B1是边长为2(单位:米)的正方形,AC=1,点D为棱AA1上的动点.