题目内容

15．某几何体的三视图如图所示，作出该几何体直观图的简图，并求该几何体的体积．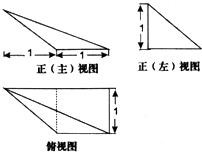

分析 根据几何体的三视图，得出该几何体是底面为正方形，高为1的四棱锥，求出它的体积，画出它的直观图．

解答 解：根据几何体的三视图，得；
该几何体是底面为正方形，高为1的四棱锥，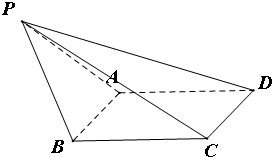
且底面正方形的边长为1；
∴该四棱锥的体积为V=$\frac{1}{3}$×12×1=$\frac{1}{3}$，
画出该四棱锥的直观图如图所示．

点评 本题考查了利用空间几何体的三视图求体积的应用问题，也考查了直观图的画法问题，是基础题目．

练习册系列答案
相关题目
5．已知向量$\overrightarrow{a}$=（cosx，-$\frac{1}{2}$），$\overrightarrow{b}$=（$\sqrt{3}$sin x，cos 2x），x∈R，设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$．
（Ⅰ）求f（x）在[0，$\frac{π}{2}$]上的最大值和最小值．
（Ⅱ）求 f（x）的单调增区间．
6．已知极坐标系的极点在直角坐标系的原点，极轴与x轴的正半轴重合，直线C1的参数方程为$\left\{\begin{array}{l}x=1+tcosα\\ y=tsinα\end{array}$（其中t为参数），曲线C2的极坐标方程为ρsin2θ=4cosθ，
（1）求当α=$\frac{π}{6}$时直线C1的普通方程及曲线C2的直角坐标方程；
（2）设F（1，0），直线C1和曲线C2相交于两点A，B，若AF=2FB，求AB的长．
3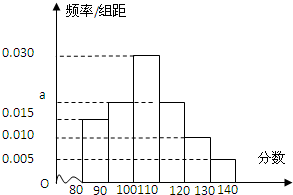．某校高一（1）班共有54人，如图是该班期中考试数学成绩的频率分布直方图，则成绩在[100，120]内的学生人数为（　　）
A．36B．27C．22D．11
10．已知点A为圆C：x2+y2=9上一动点，AM⊥x轴，垂足为M．动点N满足$\overrightarrow{ON}=\frac{{\sqrt{3}}}{3}\overrightarrow{OA}+（1-\frac{{\sqrt{3}}}{3}）\overrightarrow{OM}$，设动点N轨迹为曲线C1．
（Ⅰ）求曲线C1的方程；
（Ⅱ）斜率为-2的直线l与曲线C1交于B、D两点，求△OBD面积的最大值．
20．一个多面体的三视图如图所示，则该多面体的体积为（　　）
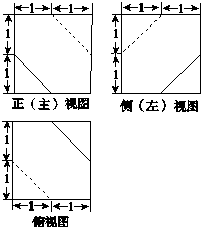
A．$\frac{23}{3}$B．$\frac{22}{3}$C．$\frac{47}{6}$D．7
7．若点P（x，y）的坐标x，y满足约束条件：$\left\{\begin{array}{l}x+y-6≤0\\ x-y+1≥0\\ x≥1\\ y≥1\end{array}\right.$，则$\frac{3x-4y}{5}$的最大值为（　　）
A．$-\frac{1}{5}$B．-1C．$\frac{11}{5}$D．11
4．已知数列{an}是等差数列，且a4=a2+4，a3=6，则数列{an}的通项公式是2n，数列$\left\{{{2^{a_n}}}\right\}$的前n项和Tn为$\frac{4}{3}（{4}^{n}-1）$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网