题目内容
6.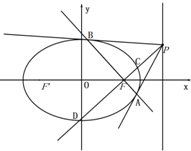 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心,以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心,以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.(1)求椭圆C的方程;
(2)过椭圆的右焦点F的直线l1与椭圆交于A、B,过F与直线l1垂直的直线l2与椭圆交于C、D,与直线l3:x=4交于P;
①求证:直线PA、PF、PB的斜率kPA,kPF,kPB成等差数列;
②是否存在常数λ使得|AB|+|CD|=λ|AB|•|CD|成立,若存在,求出λ的值,若不存在,请说明理由.
分析 (1)利用椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,可得e=$\frac{c}{a}=\frac{1}{2}$,椭圆C的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切,求得a,b的值,则椭圆方程可求;
(2)①分直线AB的斜率存在和不存在讨论,当直线的斜率不存在时,可得直线PA、PF、PB的斜率kPA,
kPF,kPB成等差数列;当直线的斜率存在时,设出直线AB的方程,和椭圆方程联立,由根与系数的关系得到A,B两点横坐标的和与积,再求出P的坐标,由kPA+kPB=2kPF得答案;
②联立AB、CD所在直线方程与椭圆方程,由弦长公式求得|AB|、|CD|的长度,代入|AB|+|CD|=λ|AB|•|CD|即可求得λ的值.
解答 (1)解:∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,∴e=$\frac{c}{a}=\frac{1}{2}$,
∵椭圆C的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.
∴b=$\frac{\sqrt{6}}{\sqrt{2}}=\sqrt{3}$,则a2=b2+c2=4,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)①证明:∵椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$的左焦点F(1,0),
当直线AB的斜率不存在时,直线AB的方程为x=1,联立直线方程和椭圆方程可得:
A(1,$\frac{3}{2}$),B(1,-$\frac{3}{2}$),此时kPA与kPB互为相反数,则kPA,kPF,kPB成等差数列;
当直线AB的斜率存在时,设过其右焦点F的直线AB的方程为:y=k(x-1),k≠0,
CD的直线方程为y=$-\frac{1}{k}(x-1)$,
由方程组$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2-8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1•x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
在CD的方程中,取x=4,得y=-$\frac{3}{k}$,∴P(4,$-\frac{3}{k}$),
则kPA+kPB=$\frac{\frac{-3}{k}-{y}_{1}}{4-{x}_{1}}+\frac{\frac{-3}{k}-{y}_{2}}{4-{x}_{2}}$
=$\frac{(-\frac{3}{k}-{y}_{1})(4-{x}_{2})+(-\frac{3}{k}-{y}_{2})(4-{x}_{1})}{(4-{x}_{1})(4-{x}_{2})}$
=$\frac{-\frac{24}{k}+(\frac{3}{k}-5k)({x}_{1}+{x}_{2})+8k+2k{x}_{1}{x}_{2}}{16-4({x}_{1}+{x}_{2})+{x}_{1}{x}_{2}}$
=$\frac{-\frac{24}{k}+(\frac{3}{k}-5k)•\frac{8{k}^{2}}{3+4{k}^{2}}+8k+2k•\frac{4{k}^{2}-12}{3+4{k}^{2}}}{16-4•\frac{8{k}^{2}}{3+4{k}^{2}}+\frac{4{k}^{2}}{3+4{k}^{2}}}$
=$\frac{-\frac{72}{k}-72k}{36({k}^{2}+1)}=-\frac{2}{k}=2{k}_{PF}$.
综上,kPA、kPF、kPB成等差数列;
②解:∵椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$的左焦点F(1,0),
设过其右焦点F的直线AB的方程为:y=k(x-1),k≠0,
由方程组$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(3+4k2)x2-8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),则x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1•x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
由弦长公式得|AB|=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}•\sqrt{(\frac{8{k}^{2}}{3+4{k}^{2}})^{2}-4•\frac{4{k}^{2}-12}{3+4{k}^{2}}}$
$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$,
同理设C(x3,y3),D(x4,y4),|CD|=$\frac{12(1+\frac{1}{{k}^{2}})}{3+4{k}^{2}}=\frac{12({k}^{2}+1)}{3{k}^{2}+4}$,
∵|AB|+|CD|=λ|AB|•|CD|,
∴λ=$\frac{|AB|+|CD|}{|AB|•|CD|}$=$\frac{1}{|AB|}+\frac{1}{|CD|}$=$\frac{3+4{k}^{2}}{12({k}^{2}+1)}+\frac{3{k}^{2}+4}{12({k}^{2}+1)}$=$\frac{7({k}^{2}+1)}{12({k}^{2}+1)}=\frac{7}{12}$.
∴存在λ=$\frac{7}{12}$,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
点评 本题重点考查直线与圆锥曲线的综合,解题的关键是直线与椭圆方程联立,利用弦长公式,综合性强,属于难题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | $\frac{3}{2}$e${\;}^{\frac{2}{3}}$ | B. | $\frac{13}{6}$e6 | C. | $\frac{1}{6}$e6 | D. | $\frac{7}{2}$e${\;}^{\frac{2}{3}}$ |
| A. | $\frac{1}{4}:\frac{1}{6}:\frac{1}{π}$ | B. | $\frac{π}{6}:\frac{π}{4}$:2 | C. | 2:3:2π | D. | $\frac{π}{6}:\frac{π}{4}$:1 |
| A. | 1 | B. | 5ln3 | C. | -5ln3 | D. | $\frac{1}{5ln3}$ |
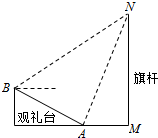 2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.
2014年足球世界杯赛上举行升旗仪式.如图,在坡度为15°的观礼台上,某一列座位所在直线AB与旗杆所在直线MN共面,在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和45°,若旗杆的高度为30米,则且座位A、B的距离为10($\sqrt{6}$-$\sqrt{2}$) 米.