题目内容
3.函数y=lg(10x+1)-$\frac{x}{2}$的奇偶性是偶函数.分析 根据奇偶性的定义进行判断即可.
解答 解:设f(x)=lg(10x+1)-$\frac{x}{2}$,
f(-x)=lg(10-x+1)+$\frac{x}{2}$=lg$\frac{1+1{0}^{x}}{1{0}^{x}}$+$\frac{x}{2}$=lg(10x+1)-x+$\frac{x}{2}$=lg(10x+1)-$\frac{x}{2}$=f(x),
故f(x)是偶函数,
故答案为:偶函数
点评 本题主要考查函数奇偶性的判断,根据对数的运算法则进行化简是解决本题的关键.

练习册系列答案
相关题目
11.公元前3世纪,古希腊欧几里得在《几何原本》里提出:“球的体积(V)与它的直径(D)的立方成正比”,此即V=kD3,欧几里得未给出k的值.17世纪日本数学家们对求球的体积的方法还不了解,他们将体积公式V=kD3中的常数k称为“立圆率”或“玉积率”.类似地,对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式V=kD3求体积(在等边圆柱中,D表示底面圆的直径;在正方体中,D表示棱长).假设运用此体积公式求得球(直径为a)、等边圆柱(底面圆的直径为a)、正方体(棱长为a)的“玉积率”分别为k1、k2、k3,那么k1:k2:k3( )
| A. | $\frac{1}{4}:\frac{1}{6}:\frac{1}{π}$ | B. | $\frac{π}{6}:\frac{π}{4}$:2 | C. | 2:3:2π | D. | $\frac{π}{6}:\frac{π}{4}$:1 |
15.已知f(x)=3x+2xf′(1),则曲线f(x)在x=0处的切线在x轴上的截距为( )
| A. | 1 | B. | 5ln3 | C. | -5ln3 | D. | $\frac{1}{5ln3}$ |
12.设随即变量X服从标准正态分布,已知P(X≤1.88)=0.97,则P(|X|≤1.88)=( )
| A. | 0.94 | B. | 0.97 | C. | 0.06 | D. | 0.03 |
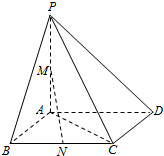 如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点
如图,四棱锥P-ABCD中,PA=AB=1,PA⊥底面ABCD,底面ABCD为正方形,且M,N分别为PA与BC的中点