题目内容
12.设函数f(x)=$\frac{1}{3}$x3-ax(a>0),g(x)=bx2+2b-1,且a=1-2b.(1)若函数y=f(x)在区间[2,+∞)内为增函数,求实数a的取值范围;
(2)当a=1时,求函数h(x)=f(x)+g(x)在区间[0,3]内的最值;
(3)当a=3时,求函数h(x)=f(x)+g(x)的极值.
分析 (1)函数y=f(x)在区间[2,+∞)内为增函数,即f′(x)≥0,分离参数,根据二次函数的性质即可求出a的范围;
(2)当a=1时,求出b=0,得到h(x)=$\frac{1}{3}$x3-x-1,x∈[0,3],根据导数函数的最值的关系即可求出答案;
(3)当a=3时,求出b=-1,得到h(x)=$\frac{1}{3}$x3-3x-x2-3,根据导数函数的极值的关系即可求出答案.
解答 解:(1)∵函数y=f(x)在区间[2,+∞)内为增函数,
∴f′(x)≥0在[2,+∞)上恒成立,
即f′(x)=x2-a≥0,
即a≤x2在[2,+∞)上恒成立,
∴a≤4,
∴实数a的取值范围为(-∞,4];
(2)∵当a=1时,a=1-2b,
∴b=0,
∴h(x)=f(x)+g(x)=$\frac{1}{3}$x3-x-1,x∈[0,3],
∴h′(x)=x2-1,
令h′(x)=0,解得x=1,
当h′(x)>0时,即1<x≤3时,函数h(x)单调递增,
当h′(x)<0时,即0≤x<1时,函数h(x)单调递减,
当x=1时,函数有极小值,也是最小值,h(x)min=h(1)=-$\frac{5}{3}$,
h(0)=-1,h(3)=5,
∴h(x)max=h(3)=5;
(3)当a=3时,a=1-2b,
∴b=-1,
∴h(x)=f(x)+g(x)=$\frac{1}{3}$x3-3x-x2-3,
∴h′(x)=x2-2x-3,
令h′(x)=0,解得x=-1,或x=3,
当h′(x)>0时,即x<-1,或x>3时,函数h(x)单调递增,
当h′(x)<0时,即-1<x<3时,函数h(x)单调递减,
∴当x=-1时函数h(x)有极大值,极大值为h(-1)=-$\frac{4}{3}$,
当x=3时,函数有极小值,极小值为h(3)=-12.
点评 本题考查了导数的函数的单调性,极值,最值的关系,以及参数的取值范围,属于中档题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | 1 | B. | 5ln3 | C. | -5ln3 | D. | $\frac{1}{5ln3}$ |
| A. | 0.94 | B. | 0.97 | C. | 0.06 | D. | 0.03 |
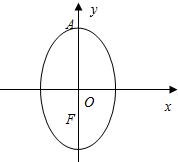 已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.
已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.