题目内容
10.sin$\frac{5π}{12}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
分析 原式中的角度变形,利用两角和与差的正弦函数公式及特殊角的三角函数值计算即可得到结果.
解答 解:sin$\frac{5π}{12}$=sin($\frac{π}{6}$+$\frac{π}{4}$)=sin$\frac{π}{6}$cos$\frac{π}{4}$+cos$\frac{π}{6}$sin$\frac{π}{4}$=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$.
故选:D.
点评 此题考查了运用诱导公式化简求值,以及两角和与差的正弦函数公式,熟练掌握公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知函数f(x)=$\frac{1}{2}$x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
| A. | $\frac{3}{2}$e${\;}^{\frac{2}{3}}$ | B. | $\frac{13}{6}$e6 | C. | $\frac{1}{6}$e6 | D. | $\frac{7}{2}$e${\;}^{\frac{2}{3}}$ |
15.已知f(x)=3x+2xf′(1),则曲线f(x)在x=0处的切线在x轴上的截距为( )
| A. | 1 | B. | 5ln3 | C. | -5ln3 | D. | $\frac{1}{5ln3}$ |
 如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=$\frac{m}{n}$,△BDM和△ABN的面积分别为S1和S2.
如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=$\frac{m}{n}$,△BDM和△ABN的面积分别为S1和S2.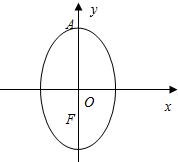 已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.
已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.