题目内容
3．求证：函数f（x）=2x+x-5在区间（1，2）有且只有一个零点．分析 先分析函数的单调性，结合零点存在定理可得答案．
解答 证明：∵f（x）=2x+x-5为增函数，
f（1）=-2＜0，f（2）=1＞0，
故f（x）在区间（1，2）内有且只有一个零点．
点评 本题考查的知识点是对数函数的图象和性质，函数的零点，难度中档．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
13．定义在R上的偶函数f（x）满足：对任意的x1，x2∈[0，+∞）（x1≠x2），有（x2-x1）[f（x2）-f（x1）]＜0．则（ ）
| A． | f（1）＜f（-2）＜f（3） | B． | f（3）＜f（1）＜f（-2） | C． | f（一2）＜f（1）＜f（3） | D． | f（3）＜f（-2）＜f（1） |
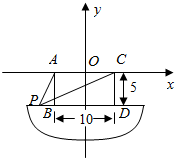船上两根高5m的桅杆相距10m，一条30m长的绳子两端系在桅杆的顶上，并按如图所示的方式绷紧，假设绳子位于两根桅杆所在的平面内，求绳子与甲板接触点P到桅杆AB的距离．
已知函数f（x）=$\left\{\begin{array}{l}{2^x}，x＜0\\ 2{（x-1）^2}-1，x≥0\end{array}\right.$．
15．等差数列{an}中an＞0，且a1+a2+…+a10=30，则a5+a6=（ ）
| A． | 3 | B． | 6 | C． | 9 | D． | 36 |