题目内容
18. 已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.(1)作出函数f(x)图象的简图,请根据图象写出函数f(x)的单调减区间;
(2)求解方程$f(x)=\frac{1}{2}$.
分析 (1)函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$的图象,从而确定函数的单调减区间;
(2)由分段函数分类讨论,从而求方程的解.
解答 解:(1)函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$的图象如下, ,
,
由图象可知,函数的单调减区间为(0,1);
(2)当x<0时,2x=$\frac{1}{2}$,解得,x=-1;
当x≥0时,2(x-1)2-1=$\frac{1}{2}$,
故x=1±$\frac{\sqrt{3}}{2}$;
故方程的解为$-1,1±\frac{{\sqrt{3}}}{2}$.
点评 本题考查了学生的作图能力及数形结合的思想应用,分段函数要分段作函数的图象.

练习册系列答案
相关题目
10.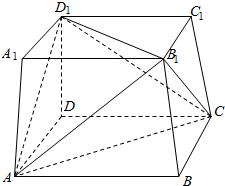 在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
 在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )
在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )| A. | 1:1 | B. | 1;$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1;2 |
8.设曲线y=ax+ln(x+1)在点(0,0)处的切线方程为y=x,则a=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
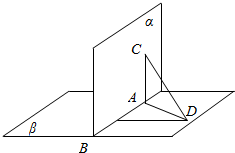 已知A,B,是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=12,AB=4,BD=3,求线段CD的长.
已知A,B,是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=12,AB=4,BD=3,求线段CD的长.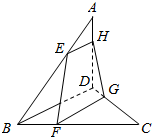 如图所示,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD,DA上的点.且满足$\frac{AE}{EB}$=$\frac{AH}{HD}$=$\frac{1}{2}$,$\frac{CF}{FB}$=$\frac{CG}{GD}$=2.
如图所示,空间四边形ABCD中,E、F、G、H分别是AB、BC、CD,DA上的点.且满足$\frac{AE}{EB}$=$\frac{AH}{HD}$=$\frac{1}{2}$,$\frac{CF}{FB}$=$\frac{CG}{GD}$=2.