题目内容
11．满足不等式3x＜$\frac{1}{27}$的实数x的取值范围是（-∞，-3）．分析 把不等式右边化为3-3，然后利用指数函数的单调性得答案．
解答 解：由${3^x}＜\frac{1}{27}$，得3x＜3-3，即x＜-3．
∴满足不等式${3^x}＜\frac{1}{27}$的实数x的取值范围是（-∞，-3）．
故答案为：（-∞，-3）．
点评 本题考查指数不等式的解法，考查了指数函数的性质，是基础题．
练习册系列答案
相关题目
1．已知f（x）是定义在（0，+∞）的函数．对任意两个不相等的正数x1，x2，都有$\frac{{x}_{2}f（{x}_{1}）-{x}_{1}f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0，记a=$\frac{f（{3}^{0.2}）}{{3}^{0.2}}$，b=$\frac{f（0．{3}^{2}）}{0．{3}^{2}}$，c=$\frac{f（lo{g}_{2}5）}{lo{g}_{2}5}$，则（ ）
| A． | a＜b＜c | B． | b＜a＜c | C． | c＜a＜b | D． | c＜b＜a |
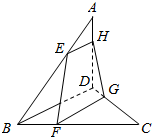如图所示，空间四边形ABCD中，E、F、G、H分别是AB、BC、CD，DA上的点．且满足$\frac{AE}{EB}$=$\frac{AH}{HD}$=$\frac{1}{2}$，$\frac{CF}{FB}$=$\frac{CG}{GD}$=2．
1．在递增等比数列{an}中，a2a16=6，a4+a14=5，则$\frac{{{a_{20}}}}{{{a_{10}}}}$等于（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | $\frac{2}{3}$或$\frac{3}{2}$ | D． | $-\frac{2}{3}$或$-\frac{3}{2}$ |