题目内容
【题目】已知等差数列{an}的前n项和为Sn ， S7=0，a3﹣2a2=12．
（1）求数列{an}的通项公式；
（2）求Sn﹣15n+50的最小值．
【答案】
（1）解：由S7=0得7a4=0…2
所以 
解得a1=﹣12，d=4…4
所以数列{an}的通项公式为an=4n﹣16
（2）解： 
…7
所以 
= 
…9
因为 
所以当n=7时，Sn﹣15n+50的最小值为2×72﹣29×7+50=﹣55
【解析】（1）利用等差数列的性质求出数列的第4项，然后求解数列的首项与公差，即可求解通项公式．（2）求出等差数列的前n项和，利用二次函数的性质，求解和的最小值．
【考点精析】掌握等差数列的前n项和公式和等差数列的性质是解答本题的根本，需要知道前n项和公式：
；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列．
练习册系列答案
相关题目
【题目】某公司2016年前三个月的利润（单位：百万元）如下：
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
（1）求利润
关于月份
的线性回归方程；
（2）试用（1）中求得的回归方程预测4月和5月的利润；
（3）试用（1）中求得的回归方程预测该公司2016年从几月份开始利润超过1000万？
相关公式：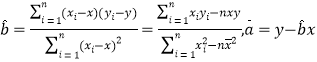
.
