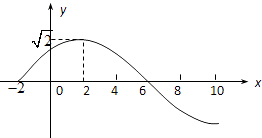Question

【题目】某班50位同学周考数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50）、[50，60）、[60，70）、[70，80）、[80，90）、[90，100]．

（1）求图中[80，90）的矩形高的值，并估计这50人周考数学的平均成绩；
（2）根据直方图求出这50人成绩的众数和中位数（精确到0.1）；
（3）从成绩在[40，60）的学生中随机选取2人，求这2人成绩分别在[40，50）、[50，60）的概率．

Answer 1

【答案】
（1）解：由频率分布直方图得：

（0.006×3+0.01+0.054+x）×10=1，

解得x=0.018．∴图中[80，90）的矩形高的值为0.018．

由频率分布直方图估计这50人周考数学的平均成绩：

=45×0.06+55×0.06+65×0.1+75×0.54+85×0.18+95×0.06=74（分）

（2）解：由频率分布直方图得这50人成绩的众数为75，

∵（0.006+0.006+0.01+0.54）×10=0.76，

∴中位数应位于第四个小矩形中，

设其底边为x，高为0.054，则0.054x=0.28，

解得x≈5.2

∴中位数M=75.2

（3）解：成绩在[40，60）的学生有（0.006+0.006）×10×50=6人，

其中成绩在[40，50）、[50，60）中各有3人，

从中随机选取2人，基本事件总数n= ，

这2人成绩分别在[40，50）、[50，60）包含的基本事件个数m= =9，

∴这2人成绩分别在[40，50）、[50，60）的概率p= =

【解析】（1）根据频率分布直方图的概率的和为1，即所求矩形的面积和为1，建立等式关系，可求出图中[80，90）的矩形高的值，由此能估计这50人周考数学的平均成绩．（2）由频率分布直方图能求出50人成绩的众数和中位数．（3）成绩在[40，60）的学生有6人，其中成绩在[40，50）、[50，60）中各有3人，由此利用等可能事件概率计算公式能求出这2人成绩分别在[40，50）、[50，60）的概率．
【考点精析】关于本题考查的频率分布直方图，需要了解频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息才能得出正确答案．