题目内容
【题目】（12分）若数列{an}是的递增等差数列，其中的a3=5，且a1，a2，a5成等比数列，
（1）求{an}的通项公式；
（2）设bn= 
，求数列{bn}的前项的和Tn．
（3）是否存在自然数m，使得
＜Tn＜
对一切n∈N*恒成立？若存在，求出m的值；
若不存在，说明理由．
【答案】（1） an= 2n﹣1；（2）
（1﹣
）=
；（3）存在；理由见解析.
【解析】试题分析：（1）由于{
}为等差数列， 
,
,
,
成等比数列，可设出数列{
}的公差为
，列方程组即可求出
;（2）在求出{
}的通项公式后，求出{
}的通项公式，再应用裂项相消法即可求
;(3)需先求Tn的值域，要使得
恒成立，则需区间(
)包含Tn的值域即可.
试题解析：
（1）在等差数列中，设公差为d≠0，
由题意
，∴
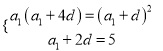，解得
．
∴an=a1+（n﹣1）d=1+2（n﹣1）=2n﹣1．
（2）由（1）知，an=2n﹣1．
则bn=
所以Tn=
（3）Tn+1﹣Tn=
,
∴{Tn}单调递增，∴Tn≥T1=
．∵Tn=
∴
≤Tn＜
, 使得
恒成立,只需
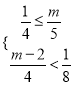解之得
,又因为m是自然数，∴m=2．
名校课堂系列答案
【题目】某学校为倡导全体学生为特困学生捐款，举行“一元钱，一片心，诚信用水”活动，学生在购水处每领取一瓶矿泉水，便自觉向捐款箱中至少投入一元钱．现统计了连续5天的售出和收益情况，如表：
售出水量x（单位：箱） | 7 | 6 | 6 | 5 | 6 |
收益y（单位：元） | 165 | 142 | 148 | 125 | 150 |
（1）求y关于x的线性回归方程；
（2）预测售出8箱水的收益是多少元？
附：回归直线的最小二乘法估计公式分别为：
=
，
=
﹣
，
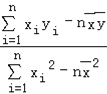【题目】甲，乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于95为正品，小于95为次品，现随机抽取这两台车床生产的零件各100件进行检测，检测结果统计如下：
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
（1）试分别估计甲机床、乙机床生产的零件为正品的概率；
（2）甲机床生产一件零件，若是正品可盈利160元，次品则亏损20元；乙机床生产一件零件，若是正品可盈利200元，次品则亏损40元，在（1）的前提下，现需生产这种零件2件，以获得利润的期望值为决策依据，应该如何安排生产最佳？