题目内容
【题目】已知点![]() ,点
,点![]() 在
在![]() 轴上,动点
轴上,动点![]() 满足
满足![]() ,且直线
,且直线![]() 与
与![]() 轴交于
轴交于![]() 点,
点, ![]() 是线段
是线段![]() 的中点.
的中点.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() 是曲线
是曲线![]() 的焦点,过
的焦点,过![]() 的两条直线
的两条直线![]() ,
, ![]() 关于
关于![]() 轴对称,且
轴对称,且![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 、
、![]() 在第一象限,若四边形
在第一象限,若四边形![]() 的面积等于
的面积等于![]() ,求直线
,求直线![]() ,
, ![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直线
;(2)直线![]() ,
, ![]() 的方程分别为
的方程分别为![]() ,
, ![]() .
.
【解析】试题分析:(1)设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,利用
,利用![]() 求动点
求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() ,与曲线
,与曲线![]() 联立,得
联立,得![]() ,结合韦达定理,即可表示四边形
,结合韦达定理,即可表示四边形![]() 的面积,求出
的面积,求出![]() ,即可求直线
,即可求直线![]() ,
, ![]() 的方程.
的方程.
试题解析:
(1)设![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
又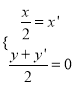 ,∴
,∴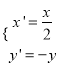 ,代入
,代入![]() ,得
,得![]() .
.
(2)由(1)知![]() ,设直线
,设直线![]() ,则
,则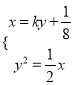 ,
,
得![]() ,
, ![]() ,
, ![]() ,
,
依题意可知,四边形![]() 是等腰梯形,
是等腰梯形,
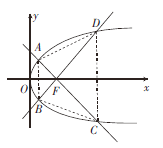
∴![]() ,
,
由![]() ,
,
即![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴直线![]() ,
, ![]() 的方程分别为
的方程分别为![]() ,
, ![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在某次测试后,一位老师从本班48同学中随机抽取6位同学,他们的语文、历史成绩如表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 |
语文成绩 | 60 | 70 | 74 | 90 | 94 | 110 |
历史成绩 | 58 | 63 | 75 | 79 | 81 | 88 |
(Ⅰ)若规定语文成绩不低于90分为优秀,历史成绩不低于80分为优秀,以频率作概率,分别估计该班语文、历史成绩优秀的人数;
(Ⅱ)用表中数据画出散点图易发现历史成绩![]() 与语文成绩
与语文成绩![]() 具有较强的线性相关关系,求
具有较强的线性相关关系,求![]() 与
与![]() 的线性回归方程(系数精确到0.1).
的线性回归方程(系数精确到0.1).
参考公式:回归直线方程是![]() ,其中
,其中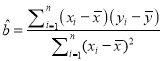 ,
, ![]()
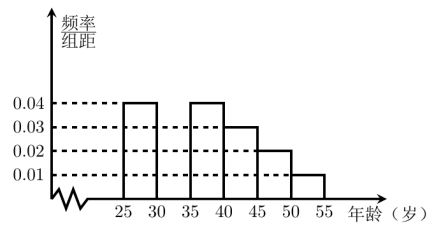
【题目】某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 |
|
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) |
| 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55] | 15 | 0.3 |
(1)补全频率分布直方图并求![]() 的值;
的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.