题目内容
10．已知f（x）=log4（4x-1）．（1）求f（x）的定义域；
（2）讨论f（x）的单调性；
（3）求f（x）在区间[$\frac{1}{2}$，2]上的值域．
分析 （1）根据4x-1＞0求解即可
（2）利用单调性的定义判断即可
（3）根据（2）问结论得出最大值，最小值即可得出值域．
解答 解：（1）4x-1＞0，所以x＞0，所以定义域是（0，+∞），
（2）f（x）在（0，+∞）上单调增，
设0＜x1＜x2，则f（x1）-f（x2）=log4（4x1-1）-log4（4x2-1）=log4$\frac{{4}^{{x}_{1}}-1}{{4}^{{x}_{2}}-1}$
又∵0＜x1＜x2，∴1＜4x1＜4x2，0＜4x1-1＜4x2-1
∴0＜$\frac{{4}^{{x}_{1}}-1}{{4}^{{x}_{2}}-1}$＜1，即log4$\frac{{4}^{{x}_{1}}-1}{{4}^{{x}_{2}}-1}$＜0
∴f（x1）＜f（x2），f（x）在（0，+∞）上单调增．
（3）∵f（x）区间[$\frac{1}{2}$，2]上单调递增，
∴最小值为log4（4${\;}^{\frac{1}{2}}$-1）=log41=0．
最大值为log4（42-1）=log415
∴值域为：[0，log415]
点评 本题考查复合函数的单调性，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
20．$\frac{7}{8}-\frac{7}{4}{sin^2}{15°}$的值等于（ ）
| A． | $\frac{7}{8}$ | B． | $\frac{7}{16}$ | C． | $\frac{{7\sqrt{3}}}{8}$ | D． | $\frac{{7\sqrt{3}}}{16}$ |
18．圆心在y轴上，且过点（3，1）的圆与x轴相切，则该圆的方程是（ ）
| A． | x2+y2+10y=0 | B． | x2+y2-10y=0 | C． | x2+y2+10x=0 | D． | x2+y2-10x=0 |
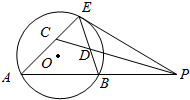如图，过圆外一点P的直线交圆O于A、B两点，PE是圆O的切线，CP平分∠APE，分别与AE、BE交于点C，D．