题目内容
2.已知函数$f(x)=\left\{\begin{array}{l}-{x^3}+{x^2},(x<1)\\ c({e^{x-1}}-1),(x≥1)\end{array}\right.$,(Ⅰ)若f[f(-1)]=e-1,求c的值;
(Ⅱ)函数y=f(x)的图象上存在两点A,B使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围;
(Ⅲ)当c=e时,讨论关于x的方程f(x)=kx(k∈R)的实根的个数.
分析 (Ⅰ)由函数$f(x)=\left\{\begin{array}{l}-{x^3}+{x^2},(x<1)\\ c({e^{x-1}}-1),(x≥1)\end{array}\right.$,将x=-1代入可得c的方程,解得c的值;
(Ⅱ)根据条件知A,B的横坐标互为相反数,分类讨论满足条件的c的范围,综合讨论结果,可得答案;
(Ⅲ)将方程转化为函数y=k与y=f(x),将方程根的问题转化为函数图象交点问题解决
解答 解:(Ⅰ)∵函数$f(x)=\left\{\begin{array}{l}-{x^3}+{x^2},(x<1)\\ c({e^{x-1}}-1),(x≥1)\end{array}\right.$,
∴f[f(-1)]=f(2)=c(e-1)=e-1,
∴c=1
(Ⅱ)∵△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,
∴A,B的横坐标互为相反数,
不妨设A(-t,t3+t2),B(t,f(t)),(t>0).
若0<t<1,则f(t)=-t3+t2,
由题意 $\overrightarrow{OA}•\overrightarrow{OB}$=0,即-t2+(t3+t2)(-t3+t2)=0,
此时t=0,不合题意,舍去;
若t≥1,则f(t)=c(et-1-1).
由于AB的中点在y轴上,且∠AOB是直角,所以B点不可能在x轴上,即t≠1.
同理由$\overrightarrow{OA}•\overrightarrow{OB}$=0,即-t2+(t3+t2)•c(et-1-1)=0,
∴c=$\frac{1}{(t+1)({e}^{t-1}-1)}$.
由于函数g(t)=$\frac{1}{(t+1)({e}^{t-1}-1)}$(t>1)的值域是(0,+∞),
∴实数c的取值范围是(0,+∞)
(III)方程f(x)=kx,知kx=$\left\{\begin{array}{l}-{x}^{3}+{x}^{2},(x<1)\\{e}^{x}-e,(x≥1)\end{array}\right.$,可知0一定是方程的根,
所以仅就x≠0时进行研究:方程等价于k=$\left\{\begin{array}{l}-{x}^{2}+{x}^{\;},(x<1,x≠0)\\{\frac{1}{x}(e}^{x}-e),(x≥1)\end{array}\right.$
构造函数g(x)=$\left\{\begin{array}{l}-{x}^{2}+{x}^{\;},(x<1,x≠0)\\{\frac{1}{x}(e}^{x}-e),(x≥1)\end{array}\right.$
对于x<1且x≠0部分,函数g(x)=-x2+x的图象是开口向下的抛物线的一部分,
当x=$\frac{1}{2}$时取得最大值$\frac{1}{4}$,其值域是(-∞,0)∪(0,$\frac{1}{4}$];
对于x≥1部分,函数g(x)=$\frac{1}{x}{(e}^{x}-e)$,由g′(x)=$\frac{{e}^{x}(x-1)+e}{{x}^{2}}$>0,知函数g(x)在[1,+∞)上单调递增.
所以,①当$k>\frac{1}{4}$或k≤0时,方程f(x)=kx有两个实根;
②当$k=\frac{1}{4}$时,方程f(x)=kx有三个实根;
③当$0<k<\frac{1}{4}$时,方程f(x)=kx有四个实根.
点评 本题主要考查函数的单调性、极值点与其导函数之间的关系,以及研究方程根的个数问题,此类问题首选的方法是图象法即构造函数利用函数图象解题,其次是直接求出所有的根

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
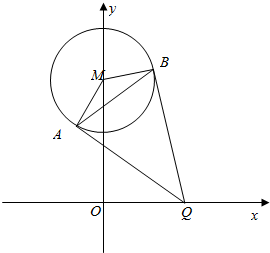 如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.
如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.