题目内容
19.己知0<a1<1,数列{an}满足:an+1=an-1+$\frac{n}{n{+}_{{a}_{n}}}$,n∈N+,则满足ai+aj(i<j,i,j∈N+)为整数的正整数组对(i,j)( )| A. | 至多一对 | B. | 至多2对 | C. | 有无穷对 | D. | 不存在 |
分析 an+1=an-1+$\frac{n}{n{+}_{{a}_{n}}}$=${a}_{n}(1-\frac{1}{{a}_{n}+n})$,n∈N+.由0<a1<1,可得an>0.又an+1-an=-$\frac{{a}_{n}}{{a}_{n}+1}$<0,可得数列{an}单调递减,而a2=${a}_{1}•\frac{{a}_{1}}{{a}_{1}+1}$$<\frac{1}{2}{a}_{1}$$<\frac{1}{2}$,因此$0<{a}_{n}<\frac{1}{2}$对n≥2时恒成立.即可得出.
解答 解:an+1=an-1+$\frac{n}{n{+}_{{a}_{n}}}$=${a}_{n}(1-\frac{1}{{a}_{n}+n})$,n∈N+,
∵0<a1<1,∴an>0,都为正.
又an+1-an=-$\frac{{a}_{n}}{{a}_{n}+1}$<0,∴数列{an}单调递减,
而${a}_{2}={a}_{1}(1-\frac{1}{{a}_{1}+1})$=${a}_{1}•\frac{{a}_{1}}{{a}_{1}+1}$$<\frac{1}{2}{a}_{1}$$<\frac{1}{2}$,因此$0<{a}_{n}<\frac{1}{2}$对n≥2时恒成立.
∴当i,j≥2时,不存在ai+aj(i<j,i,j∈N+)为整数.
只有可能a1+aj=1.
故选:A.
点评 本题考查了递推关系、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
14.为了纪念抗日战争胜利70周年,从甲、乙、丙等5名候选民警中选2名作为阅兵安保人员,为9月3号的阅兵提供安保服务,则甲、乙、丙三人中有2人被选中的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
8.下列函数中,既不是奇函数,也不是偶函数的是( )
| A. | y=x+sinx | B. | y=xsinx | C. | y=x+cosx | D. | y=xcosx |
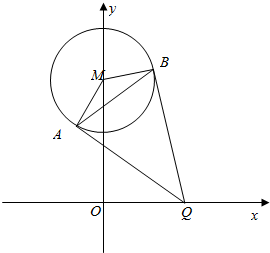 如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.
如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.