题目内容
15.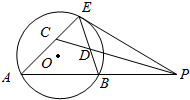 如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.
如图,过圆外一点P的直线交圆O于A、B两点,PE是圆O的切线,CP平分∠APE,分别与AE、BE交于点C,D.求证:(1)CE=DE;
(2)$\frac{CA}{CE}$=$\frac{PE}{PB}$.
分析 (1)由弦切角定理得∠A=∠BEP,由角平分线性质得到∠ECD=∠EDC,由此能证明EC=ED.
(2)由已知条件推导出△PBD∽△PEC,△PDE∽△PCA,由此能证明$\frac{CA}{CE}$=$\frac{PE}{PB}$.
解答 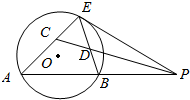 证明:(1)∵PE是圆O的切线,∴∠A=∠BEP,
证明:(1)∵PE是圆O的切线,∴∠A=∠BEP,
∵PC平分∠APE,∴∠A+∠CPA=∠BEP+∠DPE,
∵∠ECD=∠A+∠CPA,∠EDC=∠BEP+∠DPE,
∴∠ECD=∠EDC,∴EC=ED.
(2)∵∠PDB=∠EDC,∠EDC=∠ECD,∠PDB=∠PCE,
∴∠BPD=∠EPC,∴△PBD∽△PEC,
∴$\frac{PE}{PB}=\frac{PC}{PD}$,
同理,△PDE∽△PCA,∴$\frac{PC}{PD}=\frac{CA}{DE}$,
∴$\frac{CA}{CE}$=$\frac{PE}{PB}$.
点评 本题考查两条线段相等的证明,考查线段比值相等的证明,是基础题,解题时要认真审题,注意弦切角定理和三角形相似的性质定理的合理运用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
5.设a,b∈R,a+bi=$\frac{11-7i}{1-2i}$,则a+b的值为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |