题目内容
1.设两圆C1,C2都和两坐标轴相切,且都过点(3,2),则两圆心的距离C1C2=4$\sqrt{6}$.分析 圆在第一象限内,设圆心的坐标为(a,a),则有|a|=$\sqrt{(a-3)^{2}+(a-2)^{2}}$,解方程求得a值,代入两点间的距离公式可求得两圆心的距离|C1C2|的值.
解答 解:∵两圆C1、C2都和两坐标轴相切,且都过点(3,2),故圆在第一象限内,
设圆心的坐标为(a,a),则有|a|=$\sqrt{(a-3)^{2}+(a-2)^{2}}$,
∴a=5+2$\sqrt{3}$,或 a=5-2$\sqrt{3}$,故圆心为(5+2$\sqrt{3}$,5+2$\sqrt{3}$)和(5-2$\sqrt{3}$,5-2$\sqrt{3}$),
故两圆心的距离|C1C2|=4$\sqrt{6}$,
故答案为:4$\sqrt{6}$.
点评 本题考查直线和圆相切的性质,点到直线的距离公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
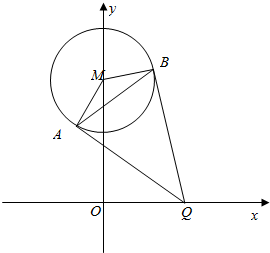 如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.
如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.