题目内容
20.一个口袋内装有大小相等的2个白球和3个黑球,从中摸出2个球.(1)求摸出2个黑球的概率;
(2)求摸出1个白球和1个黑球的概率.
分析 (1)把白球编号为1,2,黑球记为a,b,c,用列举法求得共有10种摸法.由于其中摸出两个黑球的方法有3种,由此可得摸出2个黑球的概率.
(2)摸出1个白球和1个黑球的方法有7种,由此可得摸出1个白球和1个黑球的概率.
解答 解:(1)白球编号为1,2,黑球记为a,b,c,
共有10种摸法:(1,2),(1,a),(1,b),(1,c),(2,a),(2,b),(2,c),
(a,b),(a,c),(b,c).
其中,摸出两个黑球的方法有 (a,b),(a,c),(b,c)3种,
故摸出2个黑球的概率为$\frac{3}{10}$;
(2)摸出1个白球和1个黑球的方法有:(1,a),(1,b),(1,c),(2,a),(2,b),(2,c),6种,
∴摸出1个白球和1个黑球的概率为$\frac{6}{10}$=$\frac{3}{5}$.
点评 本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
8.下列函数中,既不是奇函数,也不是偶函数的是( )
| A. | y=x+sinx | B. | y=xsinx | C. | y=x+cosx | D. | y=xcosx |
15.在平面直角坐标系中,y轴上有一点M到点A(0,0)与点B(4,2)的距离相等,则点M的坐标是( )
| A. | (0,5) | B. | (0,-5) | C. | (5,0) | D. | (-5,0) |
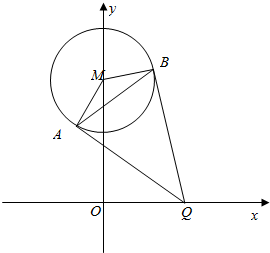 如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.
如图,已知圆M:x2+(y-4)2=4,Q是x轴上的动点,QA、QB分别切圆M于A,B两点.