题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左顶点为A,右焦点为F,且|AF|=3.
,左顶点为A,右焦点为F,且|AF|=3.
(Ⅰ)求椭圆的方程;
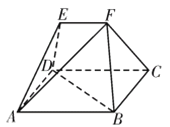
(Ⅱ)过点F做互相垂直的两条直线l1,l2分别交直线l:x=4于M,N两点,直线AM,AN分别交椭圆于P,Q两点,求证:P,F,Q三点共线.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
(Ⅰ)根据离心率和|AF|=3,可得a=2,c=1,从而求出椭圆的方程;
(Ⅱ)设l1:y=k1(x-1),联立l1和椭圆的方程,得P坐标,因为直线l1,l2垂直,同理得Q坐标.且F(1,0),所以按![]() 和
和![]() 分类讨论,判断即可.
分类讨论,判断即可.
(Ⅰ)设椭圆的半焦距为c,依题意: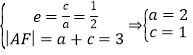 ,
,
得b2=a2-c2=3,所以椭圆的方程是![]() .
.
(Ⅱ)由题意可知,直线l1,l2的斜率均存在且不为0,A(-2,0),F(1,0),设l1,l2的斜率分别为k1,k2,则k1k2=-1.
直线l1的方程为y=k1(x-1),则M点坐标为(4,3k1),得![]() ,设直线AM的方程为
,设直线AM的方程为![]() ,
,
由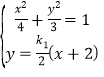 得:
得:![]()
因为x=-2是方程的根,所以![]() ,
,![]() .同理可得
.同理可得![]() .
.
当![]() ,即
,即![]() 时,可得
时,可得![]() ,又F(1,0),所以P,F,Q三点共线;
,又F(1,0),所以P,F,Q三点共线;
当![]() ,即
,即![]() ,
,![]() 时,
时,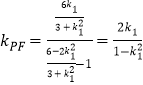 ,
,
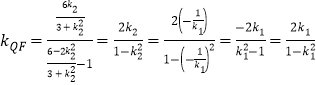 ,得kQF=kPF,所以P,F,Q三点共线;
,得kQF=kPF,所以P,F,Q三点共线;
综上所述:P,F,Q三点共线.

练习册系列答案
相关题目