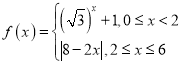题目内容
【题目】函数y=f（x），x∈[1，+∞），数列{an}满足
，
①函数f（x）是增函数；
②数列{an}是递增数列．
写出一个满足①的函数f（x）的解析式______．
写出一个满足②但不满足①的函数f（x）的解析式______．
【答案】f（x）=x2 
【解析】
本题第一个填空可用到常用的函数f（x）=x2；第二个填空要考虑到函数和对应的数列增减性不同．
由题意可知：在x∈[1，+∞）这个区间上是增函数的函数有许多，可写为：f（x）=x2．
第二个填空是找一个数列是递增数列，而对应的函数不是增函数，可写为：
．
则这个函数在[1，
]上单调递减，在[，+∞）上单调递增，
∴在[1，+∞）上不是增函数，不满足①．
而对应的数列为：
在n∈N*上越来越大，属递增数列．
故答案为：f（x）=x2；．
练习册系列答案
阅读快车系列答案
相关题目
