题目内容
【题目】如图,矩形![]() 所在平面与半圆弧
所在平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?说明理由.
?说明理由.

【答案】(1)证明见解析
(2)存在,理由见解析
【解析】分析:(1)先证![]() ,再证
,再证![]() ,进而完成证明。
,进而完成证明。
(2)判断出P为AM中点,,证明MC∥OP,然后进行证明即可。
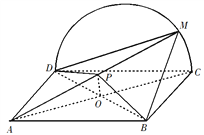
详解:(1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC![]() 平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
因为M为![]() 上异于C,D的点,且DC为直径,所以DM⊥CM.
上异于C,D的点,且DC为直径,所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM![]() 平面AMD,故平面AMD⊥平面BMC.
平面AMD,故平面AMD⊥平面BMC.
(2)当P为AM的中点时,MC∥平面PBD.
证明如下:连结AC交BD于O.因为ABCD为矩形,所以O为AC中点.
连结OP,因为P为AM 中点,所以MC∥OP.
MC![]() 平面PBD,OP
平面PBD,OP![]() 平面PBD,所以MC∥平面PBD.
平面PBD,所以MC∥平面PBD.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目