Question

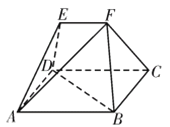
【题目】如图，在多面体中，四边形为矩形，，均为等边三角形，，．

（1）过作截面与线段交于点，使得平面，试确定点的位置，并予以证明；

（2）在（1）的条件下，求直线与平面所成角的正弦值．

Answer 1

【答案】（1）当为线段的中点时，使得平面．（2）

【解析】

试题分析：(1) 当为线段的中点时，平面．连结AC交BD于M,连结MN.利用中位线定理即可证明 ,于是平面．

(2)通过线面关系证得 ，．分别以，，的方向为，，轴的正方向，建立空间直角坐标系，用向量法求解即可.

试题解析：（1）当为线段的中点时，使得平面．

证法如下：

连接，，设，

∵四边形为矩形，

∴为的中点，

又∵为的中点，

∴为的中位线，

∴，

∵平面，平面，

∴平面，故为的中点时，使得平面．

（2）过作分别与，交于，，

因为为的中点，所以，分别为，的中点，

∵与均为等边三角形，且，

∴，连接，，则得，

∵， ，，

∴，，

∴四边形为等腰梯形．

取的中点，连接，则，

又∵，，，

∴平面，

过点作于，则，

∴ ，．

分别以，，的方向为，，轴的正方向，建立空间直角坐标系，不妨设，则由条件可得：，，，，，．

设是平面的法向量，

则即

所以可取，

由，可得，

∴直线与平面所成角的正弦值为．