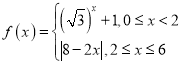题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 存在极小值点,求
存在极小值点,求![]() 的取值范围;
的取值范围;
(2)证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)先求导数,再讨论![]() 时与
时与![]() 时情况下导函数零点,根据导函数符号确定极值点取法,即得结果,(2)利用放缩法转化证
时情况下导函数零点,根据导函数符号确定极值点取法,即得结果,(2)利用放缩法转化证![]() ,(
,(![]() ),利用二次求导确定函数
),利用二次求导确定函数![]() 单调性,再根据单调性证不等式.
单调性,再根据单调性证不等式.
(1)由题意知,函数![]() 的定义域为
的定义域为![]()
![]()
①当![]() 时,令
时,令![]() ,解得
,解得![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() 是函数
是函数![]() 的极小值点,满足题意.
的极小值点,满足题意.
②当![]() 时,令
时,令![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
若![]() ,即
,即![]() 时,
时,
![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递增,无极值点,不满足题意.
上单调递增,无极值点,不满足题意.
若![]() ,即
,即![]() 时,
时,
![]() ,
,
∴![]() ,
,
又![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上恰有一个零点
上恰有一个零点![]() ,
,
当![]() 时
时![]() ,
,
当![]() 时
时![]() ,
,
∴![]() 是
是![]() 的极小值点,满足题意,
的极小值点,满足题意,
综上,![]() .
.
(2)当![]() 时
时![]()
若![]() 成立,
成立,
则![]() 必成立.
必成立.
①若![]() ,则
,则![]() ,
,![]()
∴![]() 成立
成立
∴![]() 成立.
成立.
②若![]() ,令
,令![]() ,
,
![]() ,
,
令![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
即![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() 时,
时,![]() 成立,
成立,
∴![]() 时,
时,![]() 成立,
成立,
综上,![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) |
晷影长(寸) | 135 |
|
|
|
|
节气 | 惊蛰(寒露) | 春分(秋分) | 清明(白露) | 谷雨(处暑) | 立夏(立秋) |
晷影长(寸) |
| 75.5 |
|
|
|
节气 | 小满(大暑) | 芒种(小暑) | 夏至 | ||
晷影长(寸) |
|
| 16.0 |
已知《易经》中记录的冬至晷影长为130.0寸,春分晷影长为72.4寸,那么《易经》中所记录的夏至的晷影长应为( )
A. 14.8寸B. 15.8寸C. 16.0寸D. 18.4寸