Question

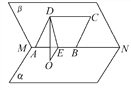
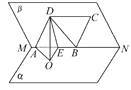
【题目】如图，已知二面角α-MN-β的大小为60°，菱形ABCD在平面β内，A，B两点在棱MN上，∠BAD=60°，E是AB的中点，DO⊥平面α，垂足为O.

(1)证明：AB⊥平面ODE.

(2)求异面直线BC与OD所成角的余弦值.

Answer 1

【答案】(1)详见解析;(2) .

【解析】试题分析:(1)由DO⊥α，ABα，所以DO⊥AB，连接BD，可得DE⊥AB,由线面垂直的判定定理即可证得成立;(2) 因为BC∥AD，所以BC与OD所成的角等于AD与OD所成的角，即∠ADO是BC与OD所成的角. 由(1)知，AB⊥平面ODE，所以AB⊥OE，又DE⊥AB，∠DEO是二面角α-MN-β的平面角，从而∠DEO=60°, 不妨设AB=2，则AD=2，在Rt△DOE中求出DO的长度,作比求出余弦值,即可求出答案.

试题解析:

(1)如图，因为DO⊥α，ABα，所以DO⊥AB，连接BD，由题设知，△ABD是正三角形，又E是AB的中点，所以DE⊥AB，DO∩DE=D，故AB⊥平面ODE.

(2)因为BC∥AD，所以BC与OD所成的角等于AD与OD所成的角，即∠ADO是BC与OD所成的角.

由(1)知，AB⊥平面ODE，所以AB⊥OE，又DE⊥AB，于是∠DEO是二面角α-MN-β的平面角，从而∠DEO=60°.

不妨设AB=2，则AD=2，易知DE=.

在Rt△DOE中，DO=DE·sin60°=，

连接AO，在Rt△AOD中，cos∠ADO===，

故异面直线BC与OD所成角的余弦值为.