题目内容
已知等差数列{an}中,前n项和Sn满足:S10+S20=1590,S10-S20=-930.
(1)求数列{an}的通项公式以及前n项和公式;
(2)是否存在三角形同时具有以下两个性质,如果存在,请求出三角形的三边长和b值;如果不存在,请说明理由.
①三边是数列{an+b}中的连续三项,其中b∈N*;
②最小角是最大角的一半.
(1)求数列{an}的通项公式以及前n项和公式;
(2)是否存在三角形同时具有以下两个性质,如果存在,请求出三角形的三边长和b值;如果不存在,请说明理由.
①三边是数列{an+b}中的连续三项,其中b∈N*;
②最小角是最大角的一半.
(1)由S10+S20=1590,S10-S20=-930,可得:S10=330,S20=1260.
由等差数列前n项和公式可得:10a1+45d=330,20a1+190d=1260,可得:a1=6,d=6,
所以an=6+(n-1)×6=6n,Sn=6n+3n(n-1);
(2)假设存在,三边为6n+b,6n+b+6,6n+b+12,设x=6n+b(x>6),则三边为x,x+6,x+12,
设最小角为α,则最大角为2α,∴cosα=
=
,cos2α=
=
∵cos2α=2cos2α-1,∴
=2[
]2-1
∴
=
,此方程无解,∴不存在.
由等差数列前n项和公式可得:10a1+45d=330,20a1+190d=1260,可得:a1=6,d=6,
所以an=6+(n-1)×6=6n,Sn=6n+3n(n-1);
(2)假设存在,三边为6n+b,6n+b+6,6n+b+12,设x=6n+b(x>6),则三边为x,x+6,x+12,
设最小角为α,则最大角为2α,∴cosα=
| x2+36x+180 |
| 2(x+6)(x+12) |
| x+30 |
| 2(x+12) |
| x2-12x-108 |
| 2x(x+6) |
| x-18 |
| 2x |
∵cos2α=2cos2α-1,∴
| x-18 |
| 2x |
| x+30 |
| 2(x+12) |
∴
| x-18 |
| x |
| -(x-6)2+648 |
| (x+12)2 |

练习册系列答案
相关题目
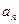 }中,
}中,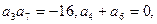 求{
求{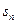 .
. 

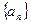 为等差数列,且
为等差数列,且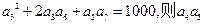 等于
等于