题目内容
等差数列{an}的前n项的和为Sn,S17>0,S18<0,则在
,
,…,
中,值最大的是______.
| S1 |
| a1 |
| S2 |
| a2 |
| S17 |
| a17 |
∵等差数列{an}中,S17>0,且S18<0
即S17=17a9>0,S18=9(a10+a9)<0
∴a10+a9<0,a9>0,∴a10<0,
∴等差数列{an}为递减数列,
故可知a1,a2,…,a9为正,a10,a11…为负;
∴S1,S2,…,S17为正,S18,S19,…为负,
∴
>0,
>0,…,
<0,
<0,…,
<0,
又∵S1<S2<…<S9,a1>a2>…>a9,
∴
,
,…,
中最大的项为
故答案为:
即S17=17a9>0,S18=9(a10+a9)<0
∴a10+a9<0,a9>0,∴a10<0,
∴等差数列{an}为递减数列,
故可知a1,a2,…,a9为正,a10,a11…为负;
∴S1,S2,…,S17为正,S18,S19,…为负,
∴
| S1 |
| a1 |
| S2 |
| a2 |
| S10 |
| a10 |
| S11 |
| a11 |
| S17 |
| a17 |
又∵S1<S2<…<S9,a1>a2>…>a9,
∴
| S1 |
| a1 |
| S2 |
| a2 |
| S17 |
| a17 |
| S9 |
| a9 |
故答案为:
| S9 |
| a9 |

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
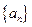 的前
的前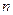 项和为
项和为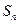 ,
, 为非零常数.已知对任意正整数
为非零常数.已知对任意正整数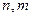 ,当
,当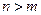 时,
时,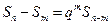 总成立.
总成立.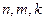 成等差数列,求证:
成等差数列,求证: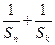 ≥
≥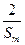 .
.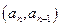 在直线
在直线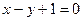 上,
上, 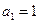 ,
,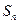 是数列
是数列 的前n项和,数列
的前n项和,数列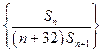 的最大值为
的最大值为