题目内容
已知函数f(x)=x+4
+4(x≥0),数列{an}满足:a1=1,an+1=f(an),(n∈N*),数列b1,b2-b1,b3-b2,…,bn-bn-1是首项为1,公比为
的等比数列.
(1)求证:数列{
}为等差数列;
(2)若cn=
•bn,求数列{cn}的前n项和Sn.
| x |
| 1 |
| 3 |
(1)求证:数列{
| an |
(2)若cn=
| an |
(1)∵函数f(x)=x+4
+4=(
+2)2(x≥0),
∴an+1=f(an)=(
+2)2,即
-
=2 (n∈N*).
∴数列{
}是以
=1为首项,公差为2的等差数列.…(4分)
(2)由(Ⅰ)得:
=1+(n-1)2=2n-1,即 an=(2n-1)2(n∈N*).…(5分)
b1=1,当n≥2时,bn-bn-1=(
)n-1,∴bn=b1+( b2-b1)+( b3-b2)+(b4-b3)+…+(bn-bn-1)
=1+
+(
)2+…+(
)n-1=
(1-
),因而 bn=
(1-
),n∈N*.…(7分)
∴cn=
•bn=(2n-1)•
(1-
),∴Sn=c1+c2+c3+…+cn=
[1+3+5+…+(2n-1)-(
+
+
+…+
)].
令Tn=
+
+
+…+
①,则
Tn=
+
+
+…+
+
②…(9分)
①-②,得
Tn=
+2(
+
+
+…+
)-
=
+
(1-
)-
,…(10分)
∴Tn=1-
.
又 1+3+5+…+(2n-1)=n2.…(11分)
∴Sn=
(n2-1+
).…(12分)
| x |
| x |
∴an+1=f(an)=(
| an |
| an+1 |
| an |
∴数列{
| an |
| a1 |
(2)由(Ⅰ)得:
| an |
b1=1,当n≥2时,bn-bn-1=(
| 1 |
| 3 |
=1+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3n |
| 3 |
| 2 |
| 1 |
| 3n |
∴cn=
| an |
| 3 |
| 2 |
| 1 |
| 3n |
| 3 |
| 2 |
| 1 |
| 3 |
| 3 |
| 32 |
| 5 |
| 33 |
| 2n-1 |
| 3n |
令Tn=
| 1 |
| 3 |
| 3 |
| 32 |
| 5 |
| 33 |
| 2n-1 |
| 3n |
| 1 |
| 3 |
| 1 |
| 32 |
| 3 |
| 33 |
| 5 |
| 34 |
| 2n-3 |
| 3n |
| 2n-1 |
| 3n+1 |
①-②,得
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 34 |
| 1 |
| 3n |
| 2n-1 |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3n-1 |
| 2n-1 |
| 3n+1 |
∴Tn=1-
| n+1 |
| 3n |
又 1+3+5+…+(2n-1)=n2.…(11分)
∴Sn=
| 3 |
| 2 |
| n+1 |
| 3n |

练习册系列答案
相关题目

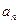 ▲ .
▲ .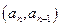 在直线
在直线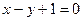 上,
上, 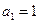 ,
,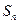 是数列
是数列 的前n项和,数列
的前n项和,数列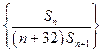 的最大值为
的最大值为 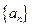 是公差不为0的等差数列,
是公差不为0的等差数列,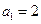 且
且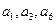 成等比数列,则
成等比数列,则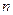 项和
项和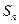 =( )
=( ) 

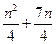
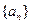 的前
的前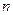 项和为
项和为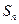 ,且
,且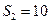 ,
,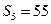 ,则过点
,则过点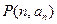 和
和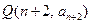
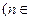 N*)的直线的斜率是__________。
N*)的直线的斜率是__________。