题目内容
9．
如图是某几何体的三视图（单位：cm），正视图是等腰梯形，俯视图中的曲线是两个同心的半圆，侧视图是直角梯形．则该几何体的体积等于（ ）| A． | 28 πcm3 | B． | 14πcm3 | C． | 7πcm3 | D． | 56πcm3 |
分析 根据几何体的三视图，得出该几何体是半个圆台，由此求出它的体积．
解答 解：根据几何体的三视图，得该几何体是下底面为半径等于4的半圆面，上底面为半径等于1的半圆面，高为4的圆台的一部分，
∴该几何体的体积为V几何体=$\frac{1}{2}$×$\frac{1}{3}$×π（12+1×4+42）×4=14πcm3．
故选：B．
点评 本题考查了利用空间几何体的三视图求体积与表面积的应用问题，是基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．定义：如果函数f（x）在[a，b]上存在x1，x2 （a＜x1＜x2＜b），满足f′（x1）=$\frac{f（b）-f（a）}{b-a}$，f′（x2）=$\frac{f′（b）-f′（a）}{b-a}$，则称数x1，x2 为[a，b]上的“对望数”函数f（x）为[a，b]上的“对望函数”，已知函数f（x）=$\frac{1}{3}{x}^{3}-{x}^{2}+m$是[0，m]上的“对望函数”，则实数m的取值范围是（ ）
| A． | （1，$\frac{3}{2}$） | B． | （1，$\frac{3}{2}$）∪（$\frac{3}{2}$，3） | C． | （2，3） | D． | （$\frac{3}{2}$，3） |
4．中心在原点，焦点在x轴上的双曲线C的离心率为$\sqrt{2}$，直线l与双曲线C交于A，B两点，线段AB中点M在第一象限，并且在抛物线y2=2px（p＞0）上，且M到抛物线焦点的距离为p，则直线l的斜率为（ ）
| A． | 2 | B． | $\frac{3}{2}$ | C． | 1 | D． | $\frac{1}{2}$ |
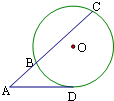如图，从圆O外一点A引圆的切线AD和割线ABC，已知AD=2$\sqrt{3}$，BC=2AB，圆心O到AC的距离为$\sqrt{5}$，则点A与圆O上的点的最短距离为$\sqrt{21}-3$．