题目内容
17.定义:如果函数f(x)在[a,b]上存在x1,x2 (a<x1<x2<b),满足f′(x1)=$\frac{f(b)-f(a)}{b-a}$,f′(x2)=$\frac{f′(b)-f′(a)}{b-a}$,则称数x1,x2 为[a,b]上的“对望数”函数f(x)为[a,b]上的“对望函数”,已知函数f(x)=$\frac{1}{3}{x}^{3}-{x}^{2}+m$是[0,m]上的“对望函数”,则实数m的取值范围是( )| A. | (1,$\frac{3}{2}$) | B. | (1,$\frac{3}{2}$)∪($\frac{3}{2}$,3) | C. | (2,3) | D. | ($\frac{3}{2}$,3) |
分析 由新定义可知f′(x1)=f′(x2)=$\frac{1}{3}$m2-m,即方程x2-2x=$\frac{1}{3}$m2-m在区间(0,m)有两个解,利用二次函数的性质可知实数m的取值范围.
解答 解:由题意可知,
在区间[0,m]存在x1,x2(0<x1<x2<m),
满足f′(x1)=$\frac{f(m)-f(0)}{m}$=$\frac{\frac{1}{3}{m}^{3}-{m}^{2}}{m}$=$\frac{1}{3}$m2-m,
∵f(x)=$\frac{1}{3}$x3-x2+m,
∴f′(x)=x2-2x,
∴方程x2-2x=$\frac{1}{3}$m2-m在区间(0,m)有两个解.
令g(x)=x2-2x-$\frac{1}{3}$m2+m,(0<x<m)
则$\left\{\begin{array}{l}{△=4+\frac{4}{3}{m}^{2}-4m>0}\\{g(0)=-\frac{1}{3}{m}^{2}+m>0}\\{g(m)=\frac{2}{3}{m}^{2}-m>0}\\{m>1}\end{array}\right.$,解得$\frac{3}{2}$<m<3,
∴实数m的取值范围是($\frac{3}{2}$,3).
故选:D.
点评 本题主要考查了导数的几何意义,二次函数的性质与方程根的关系,属于中档题.

练习册系列答案
相关题目
12.复数z满足(1+i)z=3+i,则复数z在复平面内所对应的点的坐标是( )
| A. | (1,-2) | B. | (-2,1) | C. | (-1,2) | D. | (2,-1) |
2.在区域$\left\{\begin{array}{l}0≤x≤1\\ 0≤y≤1\end{array}\right.$内任意取一点P(x,y),则x2+y2>1的概率是( )
| A. | $\frac{2π-4}{4}$ | B. | $\frac{π-2}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{4-π}{4}$ |
9.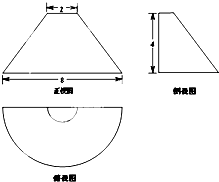 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )| A. | 28 πcm3 | B. | 14πcm3 | C. | 7πcm3 | D. | 56πcm3 |
7.已知向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(m,2),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数m等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或$-\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证: