题目内容
16.若a>b>c>0,x=$\sqrt{{a}^{2}+(b+c)^{2}}$,y=$\sqrt{{b}^{2}+(c+a)^{2}}$,z=$\sqrt{{c}^{2}+(a+b)^{2}}$,则x,y,z的大小顺序是z>y>x.分析 a>b>c>0,可得2ab>2ac>2bc,把x,y,z分别化简,即可得出.
解答 解:∵a>b>c>0,
∴2ab>2ac>2bc,
又x=$\sqrt{{a}^{2}+(b+c)^{2}}$=$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}+2bc}$,y=$\sqrt{{b}^{2}+(c+a)^{2}}$=$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}+2ac}$,z=$\sqrt{{c}^{2}+(a+b)^{2}}$=$\sqrt{{a}^{2}+{b}^{2}+{c}^{2}+2ab}$,
∴z>y>x.
故答案为:z>y>x.
点评 本题考查了不等式的性质、乘法公式的应用,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.从抛物线y2=4x图象上一点P引抛物线准线的垂线,垂足为M,且|PM|=3,设抛物线焦点为F,则△MPF周长为( )
| A. | 6+3$\sqrt{2}$ | B. | 5+2$\sqrt{3}$ | C. | 8 | D. | 6+2$\sqrt{3}$ |
9. 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )| A. | 28 πcm3 | B. | 14πcm3 | C. | 7πcm3 | D. | 56πcm3 |
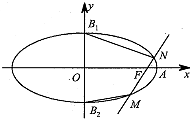 已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).