题目内容
18.某电视台推出一档游戏类综艺节目,选手面对1-5号五扇大门,依次按响门上的门铃,门铃会播放一段音乐,选手需正确回答这首歌的名字,回答正确,大门打开,并获得相应的家庭梦想基金,回答每一扇门后,选手可自由选择带着目前的奖金离开,还是继续挑战后面的门以获得更多的梦想基金,但是一旦回答错误,游戏结束并将之前获得的所有梦想基金清零;整个游戏过程中,选手有一次求助机会,选手可以询问亲友团成员以获得正确答案.1-5号门对应的家庭梦想基金依次为3000元、6000元、8000元、12000元、24000元(以上基金金额为打开大门后的累积金额,如第三扇大门打开,选手可获基金总金额为8000元);设某选手正确回答每一扇门的歌曲名字的概率为pi(i=1,2,…,5),且pi=$\frac{6-i}{7-i}$(i=1,2,…,5),亲友团正确回答每一扇门的歌曲名字的概率均为$\frac{1}{5}$,该选手正确回答每一扇门的歌名后选择继续挑战后面的门的概率均为$\frac{1}{2}$;
(1)求选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率;
(2)若选手在整个游戏过程中不使用求助,且获得的家庭梦想基金数额为X(元),求X的分布列和数学期望.
分析 (1)设事件“选手在第三扇门使用求助且最终获得12000元家庭梦想基金”为事件A.利用独立重复试验求得概率.
(2)写出X的所有可能取值并求得其概率和分布列.
解答 解:设事件“该选手回答正确第i扇门的歌曲名称”为事件Ai,“使用求助回答正确歌曲名称”为事件B,
事件“每一扇门回答正确后选择继续挑战下一扇门”为事件C;则
$P({A}_{1})=\frac{5}{6},P({A}_{2})=\frac{4}{5},P({A}_{3})=\frac{3}{4}$,$P({A}_{4})=\frac{2}{3},P({A}_{5})=\frac{1}{2}$,$P(B)=\frac{1}{5},P(C)=\frac{1}{2}$…(2分)
(1)设事件“选手在第三扇门使用求助且最终获得12000元家庭梦想基金”为事件A,则:
A=A1CA2C $\overline{{A}_{3}}BC{A}_{4}\overline{C}=\frac{5}{6}×\frac{4}{5}×\frac{1}{4}×\frac{1}{5}×\frac{2}{3}$×$(\frac{1}{2})^{4}=\frac{1}{720}$
∴选手在第三扇门使用求助且最终获得12000元家庭梦想基金的概率为$\frac{1}{720}$;…(6分)
(2)X的所有可能取值为:0,3000,6000,8000,12000,24000;
P(X=3000)=P(A1$\overline{C}$)=$\frac{5}{6}×\frac{1}{2}=\frac{5}{12}$;
P(X=6000)=P(A1 CA2 $\overline{C}$)=$\frac{5}{6}$×$\frac{4}{5}$×($\frac{1}{2}$)2=$\frac{1}{6}$;
P(X=8000)=P(A1 CA2 CA3 $\overline{C}$)=$\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×(\frac{1}{2})^{3}=\frac{1}{16}$;
P(X=12000)=P(A1 CA2 CA3 CA4 $\overline{C}$)=$\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×(\frac{1}{2})^{4}=\frac{1}{48}$;
P(X=24000)=P(A1 CA2 CA3 CA4 CA5)=$\frac{5}{6}×\frac{4}{5}×\frac{3}{4}×\frac{2}{3}×(\frac{1}{2})^{5}=\frac{1}{96}$;
P(X=0)=P($\overline{{A}_{1}}$)+P(A1C $\overline{{A}_{2}}$)+P(A1CA2C $\overline{{A}_{3}}$)+P(A1CA2CA3C $\overline{{A}_{4}}$)+P(A1CA2CA3CA4C $\overline{{A}_{5}}$)=$\frac{1}{6}+\frac{1}{12}+\frac{1}{24}+\frac{1}{48}+\frac{1}{96}=\frac{31}{96}$;
(或P(X=0)=1-(P(X=3000)+P(X=6000)+P(X=8000)+P(X=12000)+P(X=24000)
=1-$(\frac{5}{12}+\frac{1}{6}+\frac{1}{16}+\frac{1}{48}+\frac{1}{96})=1-\frac{65}{96}=\frac{31}{96}$).
∴X的分布列为:
| X | 0 | 3000 | 6000 | 8000 | 12000 | 24000 |
| P | $\frac{31}{96}$ | $\frac{5}{12}$ | $\frac{1}{6}$ | $\frac{1}{16}$ | $\frac{1}{48}$ | $\frac{1}{96}$ |
=1250+1000+500+250+250=3250(元)
∴选手获得的家庭梦想基金数额为X的数学期望为3250(元)…(12分)
点评 本题主要考查了独立重复试验和随机变量的期望,属中档题型,高考常考题型

 综合自测系列答案
综合自测系列答案 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )| A. | 28 πcm3 | B. | 14πcm3 | C. | 7πcm3 | D. | 56πcm3 |
| A. | $\frac{\sqrt{2}π}{2015}$ | B. | $\frac{2\sqrt{2}π}{2015}$ | C. | $\frac{2π}{2015}$ | D. | $\frac{4π}{2015}$ |
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或$-\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
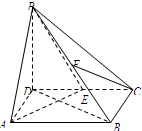 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证: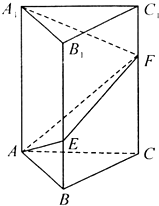 如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.
如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.