题目内容
19.设函数f(x)=|x-$\frac{1}{a}$|+|x+a|≥m.则m的最大值是2.分析 利用绝对值不等式、基本不等式,可得f(x)=|x-$\frac{1}{a}$|+|x+a|≥|a+$\frac{1}{a}$|=|a|+|$\frac{1}{a}$|≥2,利用条件,即可求出m的最大值.
解答 解:函数f(x)=|x-$\frac{1}{a}$|+|x+a|≥|a+$\frac{1}{a}$|=|a|+|$\frac{1}{a}$|≥2,
∵函数f(x)=|x-$\frac{1}{a}$|+|x+a|≥m,
∴m≤2,
∴m的最大值是2.
故答案为:2.
点评 本题考查绝对值不等式、基本不等式,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )| A. | 28 πcm3 | B. | 14πcm3 | C. | 7πcm3 | D. | 56πcm3 |
7.已知向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(m,2),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数m等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{2}$或$-\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | 0 |
14.如果函数y=|cos(ωx+$\frac{π}{4}$)|的图象关于直线x=π对称,则正实数ω的最小值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为 4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
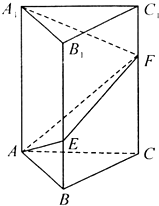 如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.
如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.