题目内容
1.设1+2i=2i(a+bi)(其中i为虚数单位,a,b∈R),则a+b的值是$\frac{1}{2}$.分析 把等式右边展开,然后利用复数相等的条件求得a,b的值,则答案可求.
解答 解:由1+2i=2i(a+bi)=-2b+2ai,得
$\left\{\begin{array}{l}{1=-2b}\\{2=2a}\end{array}\right.$,解得a=1,b=-$\frac{1}{2}$.
∴a+b=1-$\frac{1}{2}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查复数代数形式的加减运算,考查了复数相等的条件,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.复数z满足(1+i)z=3+i,则复数z在复平面内所对应的点的坐标是( )
| A. | (1,-2) | B. | (-2,1) | C. | (-1,2) | D. | (2,-1) |
9. 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
 如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )
如图是某几何体的三视图(单位:cm),正视图是等腰梯形,俯视图中的曲线是两个同心的半圆,侧视图是直角梯形.则该几何体的体积等于( )| A. | 28 πcm3 | B. | 14πcm3 | C. | 7πcm3 | D. | 56πcm3 |
13.已知f(x)=sin(2015x+$\frac{3π}{8}$)+sin(2015x-$\frac{π}{8}$)的最大值为A,若存在实数x1,x2,使得对任意实数x总有f(x1)≤f(x)≤f(x2)成立,则A|x1-x2|的最小值为( )
| A. | $\frac{\sqrt{2}π}{2015}$ | B. | $\frac{2\sqrt{2}π}{2015}$ | C. | $\frac{2π}{2015}$ | D. | $\frac{4π}{2015}$ |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为 4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
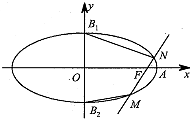 已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),其右顶点为 A(2,0),上、下顶点分别为 B1,B2.直线 A B2的斜率为$\frac{1}{2}$,过椭圆的右焦点F的直线交椭圆于 M,N两点( M,N均在y轴右侧).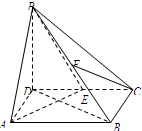 如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,AD=$\sqrt{2}$,PD⊥平面ABCD,E,F分别为CD,PB的中点.求证: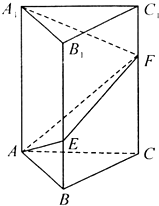 如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.
如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=AC=1,AA1=3,点E,F分别在棱BB1,CC1上,且C1F=$\frac{1}{3}$C1C,BE=$\frac{1}{3}$BB1.