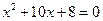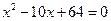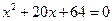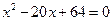题目内容
(14分)已知在数列{an}中,a1=t,a2=t2,其中t>0,x=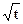 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
(Ⅱ)当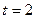 时,令
时,令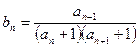 ,数列
,数列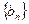 前
前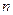 项的和为
项的和为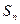 ,求证:
,求证: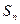
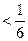
(Ⅲ)设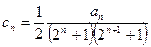 ,数列
,数列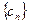 前
前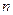 项的和为
项的和为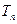 ,
, 求同时满足下列两个条件的
求同时满足下列两个条件的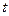 的值:(1)
的值:(1)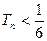 (2)对于任意的
(2)对于任意的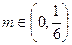 ,均存在
,均存在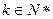 ,当
,当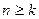 时,
时,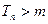
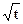 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式(Ⅱ)当
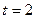 时,令
时,令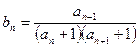 ,数列
,数列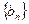 前
前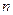 项的和为
项的和为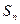 ,求证:
,求证: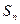
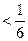
(Ⅲ)设
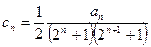 ,数列
,数列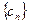 前
前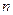 项的和为
项的和为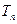 ,
, 求同时满足下列两个条件的
求同时满足下列两个条件的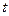 的值:(1)
的值:(1)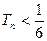 (2)对于任意的
(2)对于任意的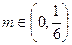 ,均存在
,均存在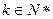 ,当
,当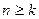 时,
时,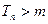
(Ⅰ)略(Ⅱ)略(Ⅲ) 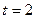
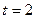
:(Ⅰ)由题意得:f′(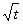 )="0 " 即3an-1t-3[(t+1)an-an+1]=0
)="0 " 即3an-1t-3[(t+1)an-an+1]=0
故an+1-an=t(an-an-1)(n≥2) 则当t≠1时,数列{an+1-an}是以t2-t为首项 t为公比的等比数列 ∴an+1-an=(t2-t)tn-1 由an+1-an=a1+(a2-a1)+(a3-a2)+…+(an-an-1) =t+(t2-t)[1+t+t2+…+tn-2] =t+(t2-t)·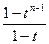 =tn此式对t=1也成立∴an=tn (n∈N
=tn此式对t=1也成立∴an=tn (n∈N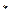 )
)
(Ⅱ)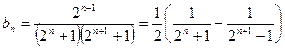
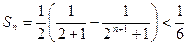
(Ⅲ) (1)当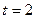 时,由Ⅱ得
时,由Ⅱ得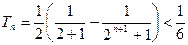
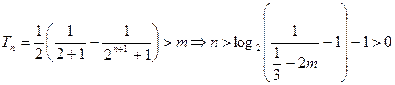
取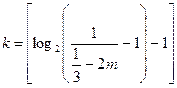 ,当
,当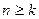 时,
时,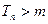
(2)当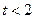 时,
时,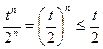 ,所以
,所以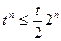
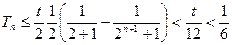
取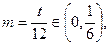 因为
因为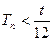 ,不存在
,不存在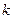 ,使得当
,使得当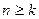 时,
时,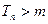
(3)当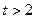 时,
时,
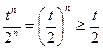 ,
,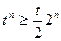
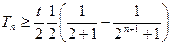 ,由(1)可知存在
,由(1)可知存在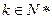 ,当
,当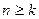 时
时
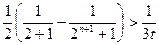 ,故存在
,故存在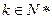 ,当
,当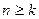 时,
时,

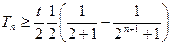
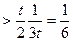
综上,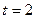
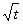 )="0 " 即3an-1t-3[(t+1)an-an+1]=0
)="0 " 即3an-1t-3[(t+1)an-an+1]=0故an+1-an=t(an-an-1)(n≥2) 则当t≠1时,数列{an+1-an}是以t2-t为首项 t为公比的等比数列 ∴an+1-an=(t2-t)tn-1 由an+1-an=a1+(a2-a1)+(a3-a2)+…+(an-an-1) =t+(t2-t)[1+t+t2+…+tn-2] =t+(t2-t)·
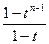 =tn此式对t=1也成立∴an=tn (n∈N
=tn此式对t=1也成立∴an=tn (n∈N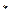 )
)
(Ⅱ)
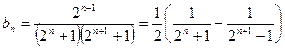
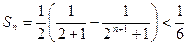
(Ⅲ) (1)当
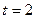 时,由Ⅱ得
时,由Ⅱ得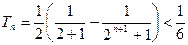
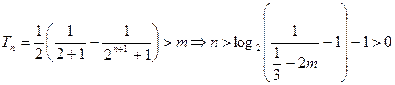
取
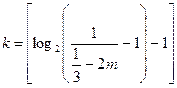 ,当
,当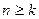 时,
时,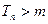
(2)当
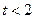 时,
时,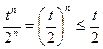 ,所以
,所以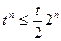
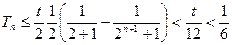
取
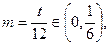 因为
因为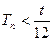 ,不存在
,不存在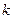 ,使得当
,使得当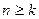 时,
时,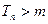
(3)当
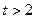 时,
时,
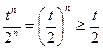 ,
,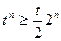
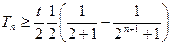 ,由(1)可知存在
,由(1)可知存在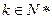 ,当
,当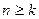 时
时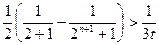 ,故存在
,故存在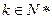 ,当
,当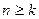 时,
时,
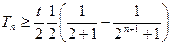
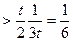
综上,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是首项为1的等差数列,且公差不为零。而等比数列
是首项为1的等差数列,且公差不为零。而等比数列 的前三项分别是
的前三项分别是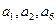 。
。 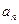 ;
; 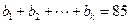 ,求正整数
,求正整数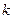 的值
的值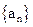 满足
满足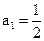 ,且
,且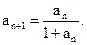
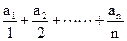
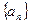 中,
中,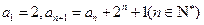 .
.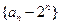 为等差数列;
为等差数列;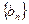 满足
满足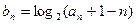 ,若
,若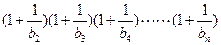
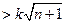 对一切
对一切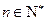 且
且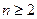 恒成立,求实数
恒成立,求实数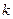 的取值范围.
的取值范围.
 ,将
,将 的图象按
的图象按 平移后得一奇函数 (Ⅰ)求当
平移后得一奇函数 (Ⅰ)求当 时函数
时函数 的值域 (Ⅱ)设数列
的值域 (Ⅱ)设数列 的通项公式为
的通项公式为
 ,
, 为其前
为其前 项的和, 求
项的和, 求 的值
的值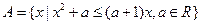 .(Ⅰ)求
.(Ⅰ)求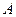 ;(Ⅱ)若
;(Ⅱ)若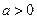 ,以
,以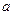 为首项,
为首项,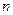 项和记为
项和记为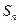 ,对于任意的
,对于任意的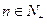 ,均有
,均有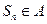 ,求
,求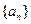 的前
的前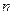 项和为
项和为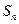 ,且
,且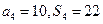 .
.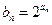 ,求数列
,求数列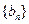 的前
的前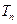 .
.