题目内容
在数列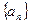 中,
中,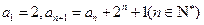 .
.
(Ⅰ)求证:数列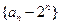 为等差数列;
为等差数列;
(Ⅱ)设数列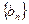 满足
满足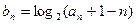 ,若
,若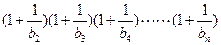
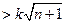 对一切
对一切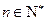 且
且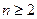 恒成立,求实数
恒成立,求实数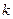 的取值范围.
的取值范围.
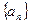 中,
中,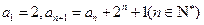 .
.(Ⅰ)求证:数列
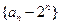 为等差数列;
为等差数列;(Ⅱ)设数列
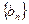 满足
满足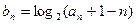 ,若
,若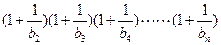
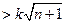 对一切
对一切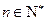 且
且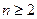 恒成立,求实数
恒成立,求实数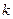 的取值范围.
的取值范围.(Ⅰ)略(Ⅱ)实数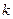 的取值范围是
的取值范围是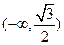
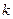 的取值范围是
的取值范围是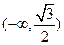
(Ⅰ) 由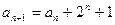 变形得:
变形得: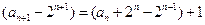
即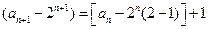
所以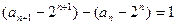 …………………4分
…………………4分
故数列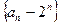 是以
是以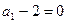 为首项,
为首项,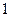 为公差的等差数列………………………5分
为公差的等差数列………………………5分
(Ⅱ)由(Ⅰ)得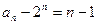 …………………………6分
…………………………6分
所以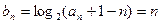 …………………………7分
…………………………7分
设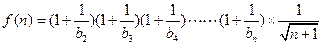 ………………8分
………………8分
则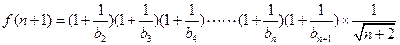
两式相除得: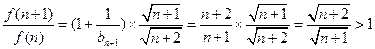 ……10分
……10分
所以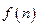 是关于
是关于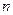 的单调递增函数,则
的单调递增函数,则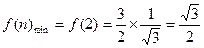
故实数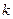 的取值范围是
的取值范围是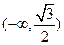 …………………………12分
…………………………12分
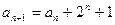 变形得:
变形得: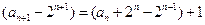
即
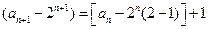
所以
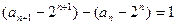 …………………4分
…………………4分故数列
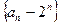 是以
是以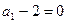 为首项,
为首项,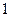 为公差的等差数列………………………5分
为公差的等差数列………………………5分(Ⅱ)由(Ⅰ)得
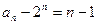 …………………………6分
…………………………6分所以
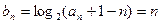 …………………………7分
…………………………7分设
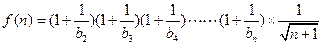 ………………8分
………………8分
则
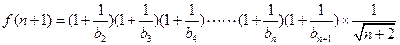
两式相除得:
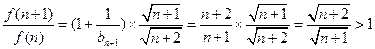 ……10分
……10分所以
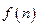 是关于
是关于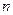 的单调递增函数,则
的单调递增函数,则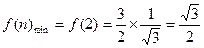
故实数
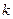 的取值范围是
的取值范围是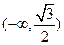 …………………………12分
…………………………12分
练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
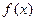 的定义域、值域均为
的定义域、值域均为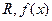 的反函数为
的反函数为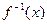 ,且对任意的
,且对任意的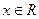 ,均有
,均有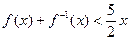 ,定义数列
,定义数列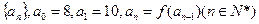
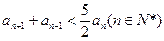
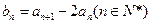 求证
求证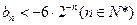
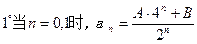 ,
,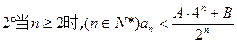 如果存在,求出A、B的值,如果不存在,说明理由。
如果存在,求出A、B的值,如果不存在,说明理由。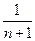 +
+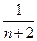 +
+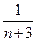 +……+
+……+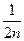 >a对于一切大于1的自然数n都成立,求实数a的取值范围。
>a对于一切大于1的自然数n都成立,求实数a的取值范围。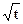 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1 (n≥2)的一个极值点(Ⅰ)求数列{an}的通项公式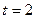 时,令
时,令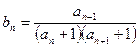 ,数列
,数列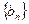 前
前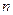 项的和为
项的和为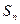 ,求证:
,求证: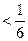
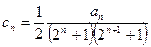 ,数列
,数列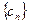 前
前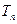 ,
, 求同时满足下列两个条件的
求同时满足下列两个条件的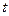 的值:(1)
的值:(1)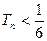 (2)对于任意的
(2)对于任意的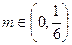 ,均存在
,均存在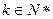 ,当
,当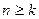 时,
时,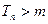
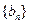 的前
的前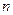 项和为
项和为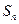 ,且
,且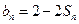 ;数列
;数列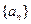 为等差数列,且
为等差数列,且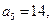
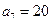 .
.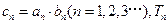 为数列
为数列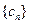 的前
的前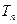 .
.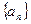 与等比数列
与等比数列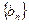 满足:
满足: ,
,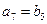 那么( )
那么( ) 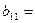
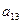
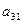
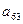
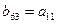
 中,
中, ,那么
,那么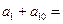 .
.