题目内容
已知直线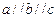 ,则直线
,则直线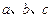 至多可以确定平面的个数为 ( )
至多可以确定平面的个数为 ( )
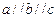 ,则直线
,则直线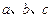 至多可以确定平面的个数为 ( )
至多可以确定平面的个数为 ( )| A.1 | B.2 | C.3 | D.4 |
C.
两平行直线可以确定一个平面,当三条平行直线不共面时可以确定三个平面.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
题目内容
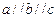 ,则直线
,则直线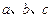 至多可以确定平面的个数为 ( )
至多可以确定平面的个数为 ( )| A.1 | B.2 | C.3 | D.4 |

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案