题目内容
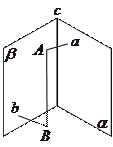
已知四面体S-ABC中,SA⊥底面ABC,△ABC是锐角三角形,H是点A在面SBC上的射影.求证:H不可能是△SBC的垂心.
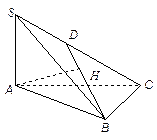
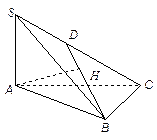
假设H是△SBC的垂心,连结BH,并延长交SC于D点,则BH⊥SC
∵AH⊥平面SBC,
∴BH是AB在平面SBC内的射影
∴SC⊥AB(三垂线定理)
又∵SA⊥底面ABC,AC是SC在面内的射影
∴AB⊥AC(三垂线定理的逆定理)
∴△ABC是Rt△与已知△ABC是锐角三角形相矛盾,于是假设不成立.
故H不可能是△SBC的垂心.
∵AH⊥平面SBC,
∴BH是AB在平面SBC内的射影
∴SC⊥AB(三垂线定理)
又∵SA⊥底面ABC,AC是SC在面内的射影
∴AB⊥AC(三垂线定理的逆定理)
∴△ABC是Rt△与已知△ABC是锐角三角形相矛盾,于是假设不成立.
故H不可能是△SBC的垂心.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
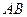 为异面直线
为异面直线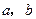 的公垂线,
的公垂线,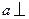 平面
平面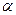 ,
,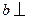 平面
平面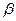 ,
,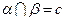 .求证:
.求证: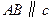 .
.
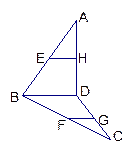
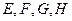 为空间四边形
为空间四边形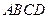 的边
的边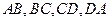 上的点,且
上的点,且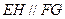 .求证:
.求证: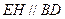 .
. 
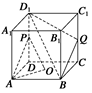
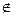 平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°求证:平面ABC⊥平面PBC
平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°求证:平面ABC⊥平面PBC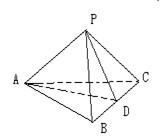
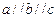 ,则直线
,则直线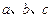 至多可以确定平面的个数为 ( )
至多可以确定平面的个数为 ( )