题目内容
已知SA、SB、SC是共点于S的且不共面的三条射线,∠BSA=∠ASC=45°,∠BSC=60°,求证:平面BSA⊥平面SAC
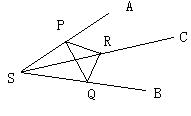

先作二面角B-SA-C的平面角,根据给定的条件,在棱S上取一点P,分别是在两个平面内作直线与棱垂直
证明:在SA上取一点P
过P作PR⊥SA交SC于R
过P作PQ⊥SA交SB于Q
∴∠QPR为二面角B-SA-C的平面角设PS=a
∵∠PSQ=45°,∠SPQ=90°
∴PQ=a,SQ=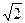 a
a
同理PR= a,SR=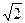 a
a
∵∠PSQ=60°,SR=SQ=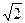 a
a
∴ΔRSQ为正三角形则RQ=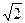 a
a
∵PR2+PQ2=2a2=QR2
∴∠QPQ=90°
∴二面角B-SA-C为90°
∴平面BSA⊥平面SAC
证明:在SA上取一点P
过P作PR⊥SA交SC于R
过P作PQ⊥SA交SB于Q
∴∠QPR为二面角B-SA-C的平面角设PS=a
∵∠PSQ=45°,∠SPQ=90°
∴PQ=a,SQ=
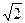 a
a同理PR= a,SR=
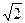 a
a∵∠PSQ=60°,SR=SQ=
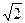 a
a∴ΔRSQ为正三角形则RQ=
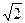 a
a∵PR2+PQ2=2a2=QR2
∴∠QPQ=90°
∴二面角B-SA-C为90°
∴平面BSA⊥平面SAC

练习册系列答案
相关题目
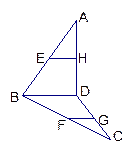
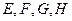 为空间四边形
为空间四边形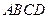 的边
的边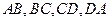 上的点,且
上的点,且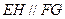 .求证:
.求证: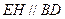 .
. 
 ABCD,O为它的对角线的交点,点P在平面α外,且PA=PC,PB=PD,求证:PO⊥α.
ABCD,O为它的对角线的交点,点P在平面α外,且PA=PC,PB=PD,求证:PO⊥α. 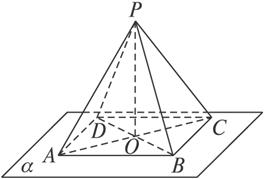
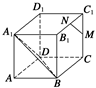
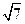
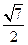
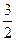
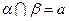 ,α⊥γ,β⊥γ,b∥α,b∥β.
,α⊥γ,β⊥γ,b∥α,b∥β.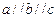 ,则直线
,则直线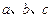 至多可以确定平面的个数为 ( )
至多可以确定平面的个数为 ( )