题目内容
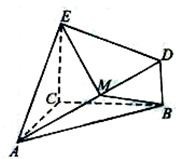
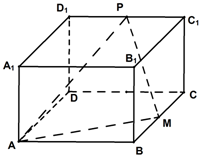
如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=
,AD=2
,P为C1D1的中点,M为BC的中点.
(Ⅰ)证明:AM⊥PM;
(Ⅱ)求AD与平面AMP所成角的正弦值;
(Ⅲ)求二面角P-AM-D的大小.
| 3 |
| 2 |
(Ⅰ)证明:AM⊥PM;
(Ⅱ)求AD与平面AMP所成角的正弦值;
(Ⅲ)求二面角P-AM-D的大小.

(Ⅰ)以D点为原点,DA、DC、DD1为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系D-xyz…(1分)
可得D(0,0,0),P(0,1,
),C(0,2,0),A(2
,0,0),M(
,2,0).
∴
=(
,2,0)-(0,1,
)=(
,1,-
),
=(
,2,0)-(2
,0,0)=(-
,2,0),
由此可得
•
=(
,1,-
)•(-
,2,0)=0,
即
⊥
,可得AM⊥PM.…(4分)
(Ⅱ)设平面PAM的一个法向量为
=(x,y,z),
则
,即
解得
,
取y=1,得
=(
,1,
),…(6分)
∴AD与平面AMP所成角θ的正弦值
sinθ=|cos<
,
>|=
=
=
.…(9分)
(Ⅲ)由(II),向量
=(
,1,
)是平面PAM的一个法向量,
∵平面AMD的法向量为
=(0,0,1),可得cos<
,
>=
=
=
可得D(0,0,0),P(0,1,
| 3 |
| 2 |
| 2 |
∴
| PM |
| 2 |
| 3 |
| 2 |
| 3 |
| AM |
| 2 |
| 2 |
| 2 |
由此可得
| PM |
| AM |
| 2 |
| 3 |
| 2 |
即
| PM |
| AM |
(Ⅱ)设平面PAM的一个法向量为
| n |
则
|
|
|
取y=1,得
| n |
| 2 |
| 3 |
∴AD与平面AMP所成角θ的正弦值
sinθ=|cos<
| DA |
| n |
|
| ||||
|
|
|(2
| ||||||||
2
|
| ||
| 3 |
(Ⅲ)由(II),向量
| n |
| 2 |
| 3 |
∵平面AMD的法向量为
| m |
| m |
| n |
| ||||
|
|
| ||
|

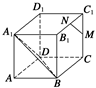
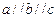 ,则直线
,则直线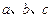 至多可以确定平面的个数为 ( )
至多可以确定平面的个数为 ( )