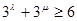题目内容
如图,己知平行四边形ABCD中,∠BAD=60°,AB=6,AD=3,G为CD中点,现将梯形ABCG沿着AG折起到AFEG.
(I)求证:直线CE∥直线BF;
(II)若直线GE与平面ABCD所成角为
.
①求证:FG⊥平面ABCD:
②求二面B一EF一A的平面角的余弦值.
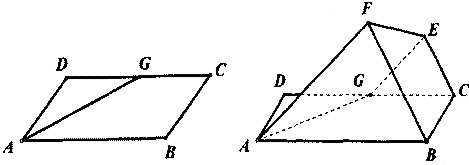
(I)求证:直线CE∥直线BF;
(II)若直线GE与平面ABCD所成角为
| π |
| 6 |
①求证:FG⊥平面ABCD:
②求二面B一EF一A的平面角的余弦值.

(Ⅰ)证明:∵AB∥CG,GE∥AF,
∴AF∥平面CGE,AB∥平面CGE,
∴平面ABF∥平面CGE,
∵直线BC∩AG=K,
∴K∈直线EF,
∴EF与BC共面,
所以,直线CE∥直线BF.
(Ⅱ)①∵∠BAD=60°,AB=6,AD=3,G为CD中点,
∴BG⊥AG,∴FG⊥AG,
∵直线GE与平面ABCD所成的角为
,而GE∥AF,
∴直线AF与平面ABCD所成的角为
,
∴F到平面ABCD的距离为3,
所以FG⊥平面ABCD.
②∵FG⊥平面ABCD,
∴FG⊥BG,∴BG⊥平面AGEF,
作GH⊥EF交EF于H,连接BH,得BH⊥EF,
∴∠BHG为B-EF-A的平面角,
∵BG=3,GH=
,tan∠BHG=
=
,
∴cos∠BHG=
,
所以二面B一EF一A的平面角的余弦值为
.

∴AF∥平面CGE,AB∥平面CGE,
∴平面ABF∥平面CGE,
∵直线BC∩AG=K,
∴K∈直线EF,
∴EF与BC共面,
所以,直线CE∥直线BF.
(Ⅱ)①∵∠BAD=60°,AB=6,AD=3,G为CD中点,
∴BG⊥AG,∴FG⊥AG,
∵直线GE与平面ABCD所成的角为
| π |
| 6 |
∴直线AF与平面ABCD所成的角为
| π |
| 6 |
∴F到平面ABCD的距离为3,
所以FG⊥平面ABCD.
②∵FG⊥平面ABCD,
∴FG⊥BG,∴BG⊥平面AGEF,
作GH⊥EF交EF于H,连接BH,得BH⊥EF,
∴∠BHG为B-EF-A的平面角,
∵BG=3,GH=
3
| ||
| 2 |
| BG |
| GH |
2
| ||
| 3 |
∴cos∠BHG=
| ||
| 7 |
所以二面B一EF一A的平面角的余弦值为
| ||
| 7 |


练习册系列答案
相关题目
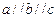 ,则直线
,则直线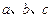 至多可以确定平面的个数为 ( )
至多可以确定平面的个数为 ( )


 是已知的平面向量,向量
是已知的平面向量,向量 ,
,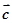 在同一平面内且两两不共线,有如下四个命题:
在同一平面内且两两不共线,有如下四个命题: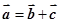 ;
; 和
和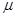 ,使
,使 ;
; =2,存在单位向量
=2,存在单位向量