题目内容
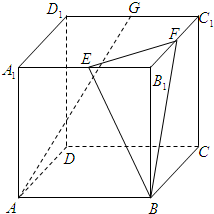
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为A1B1、B1C1、C1D1的中点.
(1)求异面直线AG与BF所成角的余弦值;
(2)求证:AG∥平面BEF;
(3)试在棱BB1上找一点M,使DM⊥平面BEF,并证明你的结论.
(1)求异面直线AG与BF所成角的余弦值;
(2)求证:AG∥平面BEF;
(3)试在棱BB1上找一点M,使DM⊥平面BEF,并证明你的结论.

(1)以D为坐标原点,DA,DC,DD1分别作为x轴,y轴和z轴建立空间直角坐标系,
则A(1,0,0),B(1,1,0),E(1,
,1),F(
,1,1),G(0,
,1),
∴
=(-1,
,1),
=(-
,0,1),
∴cos<
,
>=
=
故异面直线AG与BF所成角的余弦值为
.
(2)∵
=(-
,
,0),
=(-
,0,1),
而
=(-1,
,1),∴
=
+
,
故
与平面BEF共面,
又因为AG不在平面BEF内,
∴AG∥平面BEF.
(3)设M(1,1,m),则
=(1,1,m)
由
•
=0,
•
=0,
∴-
+m=0⇒m=
,
所以M为棱BB1的中点时,DM⊥平面BEF.
则A(1,0,0),B(1,1,0),E(1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AG |
| 1 |
| 2 |
| BF |
| 1 |
| 2 |
∴cos<
| AG |
| BF |
| ||||||
|
2
| ||
| 5 |
故异面直线AG与BF所成角的余弦值为
2
| ||
| 5 |
(2)∵
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| BF |
| 1 |
| 2 |
而
| AG |
| 1 |
| 2 |
| AG |
| EF |
| BF |
故
| AG |
又因为AG不在平面BEF内,
∴AG∥平面BEF.
(3)设M(1,1,m),则
| DM |
由
| DM |
| EF |
| DM |
| BF |
∴-
| 1 |
| 2 |
| 1 |
| 2 |
所以M为棱BB1的中点时,DM⊥平面BEF.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
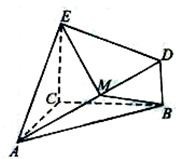
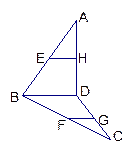
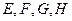 为空间四边形
为空间四边形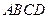 的边
的边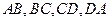 上的点,且
上的点,且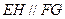 .求证:
.求证: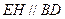 .
. 

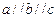 ,则直线
,则直线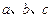 至多可以确定平面的个数为 ( )
至多可以确定平面的个数为 ( )