题目内容
已知函数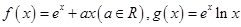 (e为自然对数的底数).
(e为自然对数的底数).
(1)设曲线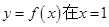 处的切线为
处的切线为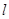 ,若
,若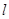 与点(1,0)的距离为
与点(1,0)的距离为 ,求a的值;
,求a的值;
(2)若对于任意实数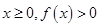 恒成立,试确定
恒成立,试确定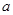 的取值范围;
的取值范围;
(3)当 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
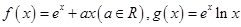 (e为自然对数的底数).
(e为自然对数的底数).(1)设曲线
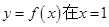 处的切线为
处的切线为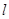 ,若
,若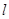 与点(1,0)的距离为
与点(1,0)的距离为 ,求a的值;
,求a的值;(2)若对于任意实数
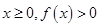 恒成立,试确定
恒成立,试确定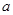 的取值范围;
的取值范围;(3)当
 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.(1)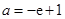 或
或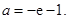 (2)
(2)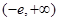 (3)不存在
(3)不存在
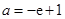 或
或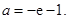 (2)
(2)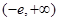 (3)不存在
(3)不存在试题分析:
(1)该问切点横坐标已知,则利用切点在曲线上,带入曲线
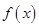 即可得到切点的纵坐标,对
即可得到切点的纵坐标,对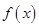 进行求导并得到在切点处的导函数值即为切线的斜率,有切线的斜率,切线又过切点,利用直线的点斜式即可求的切线的方程,利用点到直线的距离公式结合条件点
进行求导并得到在切点处的导函数值即为切线的斜率,有切线的斜率,切线又过切点,利用直线的点斜式即可求的切线的方程,利用点到直线的距离公式结合条件点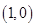 到切线的距离为
到切线的距离为 即可求的参数
即可求的参数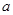 的值.
的值.(2)该问为恒成立问题可以考虑分离参数法,即把参数a与x进行分离得到
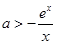 ,则
,则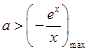 ,再利用函数的导函数研究函数
,再利用函数的导函数研究函数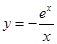 在区间
在区间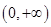 的最大值,即可求的a的取值范围.
的最大值,即可求的a的取值范围.(3)根据极值的定义,函数
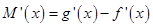 在区间
在区间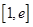 有零点且在零点附近的符号不同,求导可得
有零点且在零点附近的符号不同,求导可得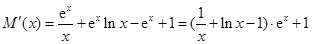 ,设
,设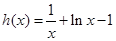 ,求
,求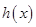 求导可以得到
求导可以得到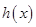 的导函数在区间
的导函数在区间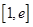 恒为正数,则函数
恒为正数,则函数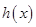 在区间
在区间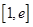 上是单调递增,即可得到函数
上是单调递增,即可得到函数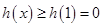 进而得到
进而得到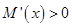 恒成立,即
恒成立,即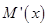 在区间
在区间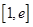 上没有零点,进而函数
上没有零点,进而函数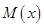 没有极值.
没有极值.试题解析:
(1)
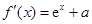 ,
,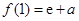 .
.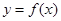 在
在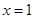 处的切线斜率为
处的切线斜率为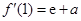 , 1分
, 1分∴切线
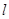 的方程为
的方程为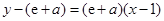 ,即
,即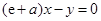 . 3分
. 3分又切线
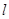 与点
与点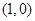 距离为
距离为 ,所以
,所以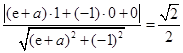 ,
,解之得,
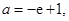 或
或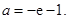 5分
5分(2)∵对于任意实数
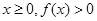 恒成立,
恒成立,∴若
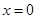 ,则
,则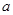 为任意实数时,
为任意实数时,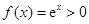 恒成立; 6分
恒成立; 6分若
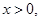
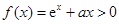 恒成立,即
恒成立,即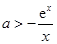 ,在
,在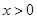 上恒成立, 7分
上恒成立, 7分设
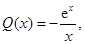 则
则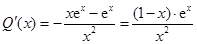 , 8分
, 8分当
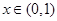 时,
时,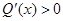 ,则
,则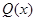 在
在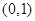 上单调递增;
上单调递增;当
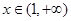 时,
时,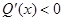 ,则
,则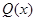 在
在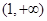 上单调递减;
上单调递减;所以当
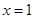 时,
时,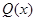 取得最大值,
取得最大值,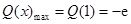 , 9分
, 9分所以
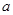 的取值范围为
的取值范围为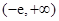 .
.综上,对于任意实数
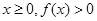 恒成立的实数
恒成立的实数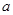 的取值范围为
的取值范围为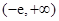 . 10分
. 10分(3)依题意,
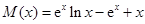 ,
,所以
 , 2分
, 2分设
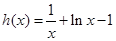 ,则
,则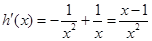 ,当
,当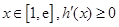 ,
,故
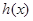 在
在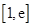 上单调增函数,因此
上单调增函数,因此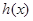 在
在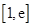 上的最小值为
上的最小值为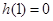 ,
,即
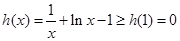 , 12分
, 12分又
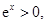 所以在
所以在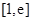 上,
上,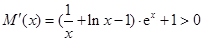 ,
,即
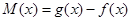 在
在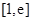 上不存在极值. 14分
上不存在极值. 14分
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
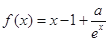 (
(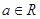 ,
,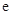 为自然对数的底数).
为自然对数的底数).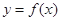 在点
在点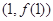 处的切线平行于
处的切线平行于 轴,求
轴,求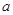 的值;
的值;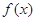 的极值;
的极值;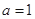 的值时,若直线
的值时,若直线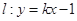 与曲线
与曲线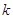 的最大值.
的最大值.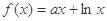 ,其中a为常数.
,其中a为常数.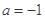 时,求
时,求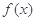 的最大值;
的最大值;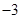 ,求a的值;
,求a的值;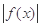 =
=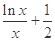 是否有实数解.
是否有实数解.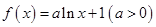 .
.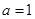 且
且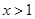 时,证明:
时,证明: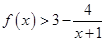 ;
;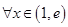 ,
,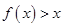 恒成立,求实数
恒成立,求实数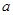 的取值范围;
的取值范围;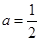 时,证明:
时,证明: .
.
 ,求
,求 的极大值点;
的极大值点; 且
且 的取值范围.
的取值范围. 与函数
与函数 在点
在点 处有公共的切线,设
处有公共的切线,设
 .
. 的值
的值 在区间
在区间 上的最小值.
上的最小值.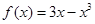 的单调减区间是
的单调减区间是  的导函数为f¢(x),则f¢(1)的值为 .
的导函数为f¢(x),则f¢(1)的值为 .