题目内容
设f(x)=(ax+b)sinx+(cx+d)cosx,若已知f′(x)=xcosx,则f(x)=( )
| A.xsinx |
| B.xsinx-xcosx |
| C.xsinx+cosx |
| D.xcosx |
C
∵f′(x)=[(ax+b)sinx]′+[(cx+d)cosx]′
=(ax+b)′sinx+(ax+b)(sinx)′+(cx+d)′cosx+(cx+d)(cosx)′
=asinx+(ax+b)cosx+ccosx-(cx+d)sinx
=(a-d-cx)sinx+(ax+b+c)cosx.
为使f′(x)=xcosx,应满足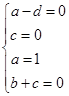
解方程组,得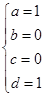
从而可知,f(x)=xsinx+cosx.
=(ax+b)′sinx+(ax+b)(sinx)′+(cx+d)′cosx+(cx+d)(cosx)′
=asinx+(ax+b)cosx+ccosx-(cx+d)sinx
=(a-d-cx)sinx+(ax+b+c)cosx.
为使f′(x)=xcosx,应满足
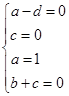
解方程组,得
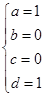
从而可知,f(x)=xsinx+cosx.

练习册系列答案
相关题目
 .
. 上总存在相异的两点
上总存在相异的两点 ,使得曲线
,使得曲线 .
.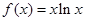 ,
,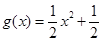 .
.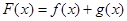 ,求函数
,求函数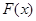 的图像在
的图像在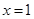 处的切线方程;
处的切线方程;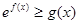 对任意的
对任意的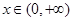 恒成立;
恒成立;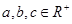 ,且
,且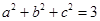 ,求证:
,求证: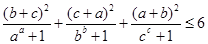 .
.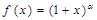 的定义域是
的定义域是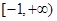 ,其中常数
,其中常数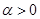 .(注:
.(注: 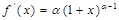
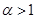 ,求
,求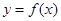 的过原点的切线方程.
的过原点的切线方程.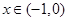 ,恒有
,恒有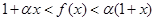 .
.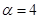 时,求最大实数
时,求最大实数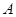 ,使不等式
,使不等式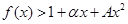 对
对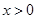 恒成立.
恒成立.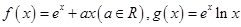 (e为自然对数的底数).
(e为自然对数的底数).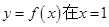 处的切线为
处的切线为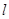 ,若
,若 ,求a的值;
,求a的值;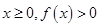 恒成立,试确定
恒成立,试确定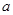 的取值范围;
的取值范围; 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由. (
( ,
, ).
). 时,求曲线
时,求曲线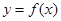 在点
在点 处切线的方程;
处切线的方程; 的单调区间;
的单调区间; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.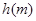 与起跳后的时间
与起跳后的时间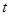
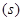 存在函数关系
存在函数关系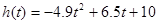 ,则瞬时速度为0
,则瞬时速度为0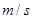 的时刻是( )
的时刻是( )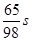
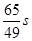
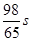
 在点(1,1)处的切线与
在点(1,1)处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,则
,则 的值为
的值为

