题目内容
已知函数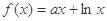 ,其中a为常数.
,其中a为常数.
(1)当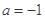 时,求
时,求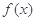 的最大值;
的最大值;
(2)若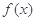 在区间(0,e]上的最大值为
在区间(0,e]上的最大值为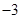 ,求a的值;
,求a的值;
(3)当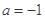 时,试推断方程
时,试推断方程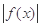 =
=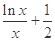 是否有实数解.
是否有实数解.
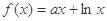 ,其中a为常数.
,其中a为常数.(1)当
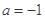 时,求
时,求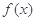 的最大值;
的最大值;(2)若
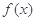 在区间(0,e]上的最大值为
在区间(0,e]上的最大值为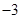 ,求a的值;
,求a的值;(3)当
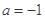 时,试推断方程
时,试推断方程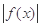 =
=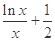 是否有实数解.
是否有实数解.(1)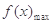 =f(1)=-1;(2)a=
=f(1)=-1;(2)a=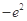 ;(3)方程|f(x)|=
;(3)方程|f(x)|=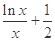 没有实数解.
没有实数解.
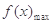 =f(1)=-1;(2)a=
=f(1)=-1;(2)a=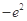 ;(3)方程|f(x)|=
;(3)方程|f(x)|=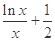 没有实数解.
没有实数解.试题分析:(1)当a=-1时,f(x)=-x+lnx,f′(x)=-1+
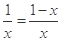
由0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
知f(x)在(0,1)上是增函数,在(1,+∞)上是减函数,从而
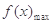 =f(1)=-1.
=f(1)=-1.(2)利用导数确定函数的最大值得,
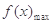 =f
=f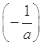 =-1+ln
=-1+ln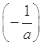
由-1+ln
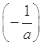 =-3,即得a=
=-3,即得a=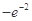 .
.(3)由(1)知当a=-1时
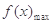 =f(1)=-1,可知|f(x)|≥1;
=f(1)=-1,可知|f(x)|≥1;应用导数研究g(x)=
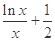 ,得到
,得到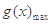 =g(e)=
=g(e)=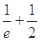 <1,即g(x)<1,
<1,即g(x)<1,根据|f(x)|>g(x),即|f(x)|>
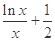 知方程|f(x)|=
知方程|f(x)|=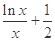 没有实数解.
没有实数解.试题解析:(1)当a=-1时,f(x)=-x+lnx,f′(x)=-1+
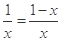
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数,
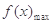 =f(1)=-14分
=f(1)=-14分(2)∵f′(x)=a+
 ,x∈(0,e],
,x∈(0,e], ∈
∈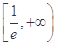
①若a≥
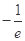 ,则f′(x)≥0,f(x)在(0,e]上增函数
,则f′(x)≥0,f(x)在(0,e]上增函数∴
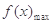 =f(e)=ae+1≥0.不合题意 5分
=f(e)=ae+1≥0.不合题意 5分②若a<
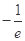 ,则由f′(x)>0
,则由f′(x)>0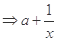 >0,即0<x<
>0,即0<x<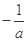
由f(x)<0
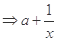 <0,即
<0,即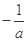 <x≤e.从而f(x)在
<x≤e.从而f(x)在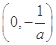 上增函数,在
上增函数,在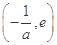 为减函数
为减函数∴
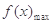 =f
=f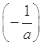 =-1+ln
=-1+ln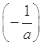
令-1+ln
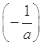 =-3,则ln
=-3,则ln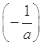 =-2∴
=-2∴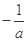 =
=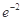 ,即a=
,即a=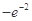 .
.∵
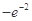 <
<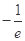 ,
,∴a=
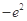 为所求 8分
为所求 8分(3)由(1)知当a=-1时
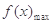 =f(1)=-1,
=f(1)=-1,∴|f(x)|≥1
又令g(x)=
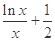 ,g′(x)=
,g′(x)=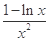 ,令g′(x)=0,得x=e,
,令g′(x)=0,得x=e,当0<x<e时,g′(x)>0,g(x)在(0,e)单调递增;当x>e时,g′(x)<0,g(x)在(e,+∞)单调递减∴
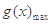 =g(e)=
=g(e)=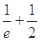 <1,∴g(x)<1
<1,∴g(x)<1∴|f(x)|>g(x),即|f(x)|>
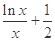 ∴方程|f(x)|=
∴方程|f(x)|=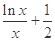 没有实数解. 12分
没有实数解. 12分
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
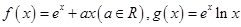 (e为自然对数的底数).
(e为自然对数的底数).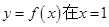 处的切线为
处的切线为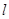 ,若
,若 ,求a的值;
,求a的值;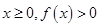 恒成立,试确定
恒成立,试确定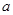 的取值范围;
的取值范围; 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由. 是自然对数的底数,函数
是自然对数的底数,函数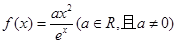 .
. 的单调递增区间;
的单调递增区间;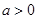 时,函数
时,函数 ,求
,求 的值.
的值.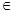 R).
R).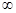 )上是减函数,求实数a的取值范围.
)上是减函数,求实数a的取值范围.
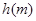 与起跳后的时间
与起跳后的时间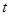
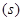 存在函数关系
存在函数关系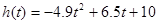 ,则瞬时速度为0
,则瞬时速度为0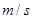 的时刻是( )
的时刻是( )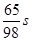
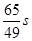
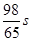
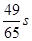
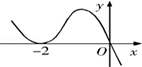
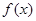 的导数为
的导数为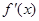 ,且
,且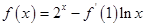 ,则
,则 的值是 .
的值是 .