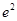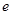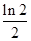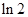题目内容
已知函数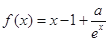 (
(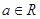 ,
,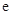 为自然对数的底数).
为自然对数的底数).
(1)若曲线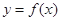 在点
在点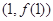 处的切线平行于
处的切线平行于 轴,求
轴,求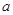 的值;
的值;
(2)求函数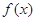 的极值;
的极值;
(3)当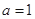 的值时,若直线
的值时,若直线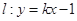 与曲线
与曲线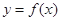 没有公共点,求
没有公共点,求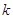 的最大值.
的最大值.
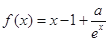 (
(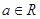 ,
,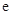 为自然对数的底数).
为自然对数的底数).(1)若曲线
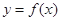 在点
在点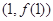 处的切线平行于
处的切线平行于 轴,求
轴,求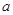 的值;
的值;(2)求函数
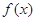 的极值;
的极值;(3)当
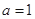 的值时,若直线
的值时,若直线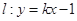 与曲线
与曲线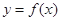 没有公共点,求
没有公共点,求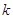 的最大值.
的最大值.(1)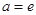 .;(2)当
.;(2)当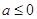 时,函数
时,函数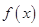 无极小值;当
无极小值;当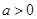 ,
,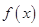 在
在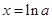 处取得极小值
处取得极小值 ,无极大值.;(3)
,无极大值.;(3)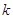 的最大值为
的最大值为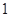 .
.
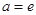 .;(2)当
.;(2)当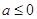 时,函数
时,函数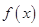 无极小值;当
无极小值;当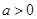 ,
,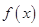 在
在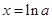 处取得极小值
处取得极小值 ,无极大值.;(3)
,无极大值.;(3)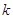 的最大值为
的最大值为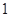 .
.试题分析:(1)由于曲线
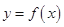 在点
在点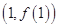 处的切线平行于
处的切线平行于 轴,所以
轴,所以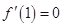 .求导解方程即可得
.求导解方程即可得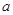 的值.(2)由于函数中含参数
的值.(2)由于函数中含参数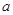 ,故需要分情况讨论.求导得:
,故需要分情况讨论.求导得: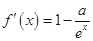 ,分情况求出函数的单调区间即可得函数的极值;(3)当
,分情况求出函数的单调区间即可得函数的极值;(3)当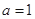 时,
时,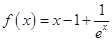 .直线
.直线 :
: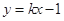 与曲线
与曲线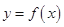 没有公共点等价于关于
没有公共点等价于关于 的方程
的方程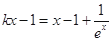 在
在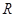 上没有实数解.一般地考虑分离参数
上没有实数解.一般地考虑分离参数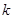 .即变形为:
.即变形为: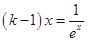 (*)在
(*)在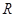 上没有实数解.当
上没有实数解.当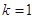 时,方程(*)可化为
时,方程(*)可化为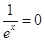 ,在
,在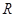 上没有实数解.当
上没有实数解.当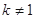 时,方程(*)化为
时,方程(*)化为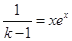 .令
.令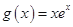 ,利用导数求出
,利用导数求出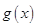 的取值范围即可得
的取值范围即可得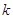 的取值范围.
的取值范围.试题解析:(1)由
 ,得
,得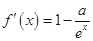 .
.又曲线
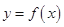 在点
在点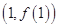 处的切线平行于
处的切线平行于 轴,
轴,得
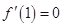 ,即
,即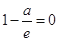 ,解得
,解得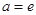 .
.(2)
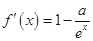 ,
,①当
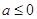 时,
时, ,
,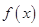 为
为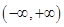 上的增函数,所以函数
上的增函数,所以函数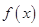 无极值.
无极值.②当
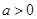 时,令
时,令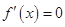 ,得
,得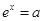 ,
,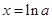 .
.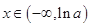 ,
,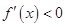 ;
;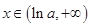 ,
, .
.所以
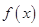 在
在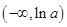 上单调递减,在
上单调递减,在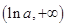 上单调递增,
上单调递增,故
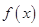 在
在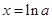 处取得极小值,且极小值为
处取得极小值,且极小值为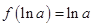 ,无极大值.
,无极大值.综上,当
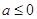 时,函数
时,函数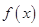 无极小值;
无极小值;当
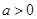 ,
,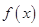 在
在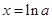 处取得极小值
处取得极小值 ,无极大值.
,无极大值.(3)当
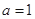 时,
时,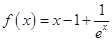 .
.直线
 :
: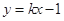 与曲线
与曲线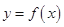 没有公共点,
没有公共点,等价于关于
 的方程
的方程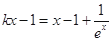 在
在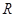 上没有实数解,即关于
上没有实数解,即关于 的方程:
的方程: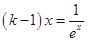 (*)
(*)在
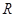 上没有实数解.
上没有实数解.①当
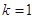 时,方程(*)可化为
时,方程(*)可化为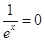 ,在
,在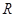 上没有实数解.
上没有实数解.②当
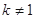 时,方程(*)化为
时,方程(*)化为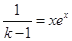 .
.令
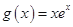 ,则有
,则有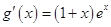 .
.令
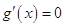 ,得
,得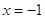 ,
,当
 变化时,
变化时,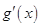 的变化情况如下表:
的变化情况如下表: | 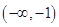 | 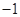 | 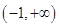 |
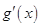 |  | 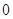 | 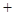 |
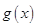 | 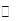 | 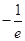 | 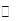 |
当
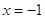 时,
时,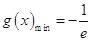 ,同时当
,同时当 趋于
趋于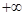 时,
时,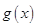 趋于
趋于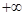 ,
,从而
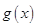 的取值范围为
的取值范围为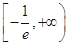 .所以当
.所以当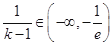 时,方程(*)无实数解,解得
时,方程(*)无实数解,解得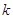 的取值范围是
的取值范围是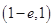 .
.综上,得
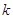 的最大值为
的最大值为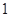 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
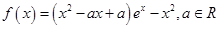 .
.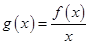 ,当
,当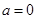 时,讨论
时,讨论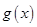 的单调性;
的单调性;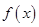 在
在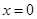 处取得极小值,求
处取得极小值,求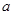 的取值范围.
的取值范围.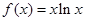 ,
,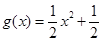 .
.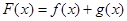 ,求函数
,求函数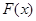 的图像在
的图像在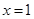 处的切线方程;
处的切线方程;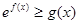 对任意的
对任意的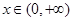 恒成立;
恒成立;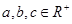 ,且
,且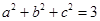 ,求证:
,求证: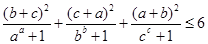 .
.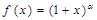 的定义域是
的定义域是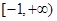 ,其中常数
,其中常数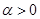 .(注:
.(注: 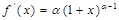
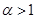 ,求
,求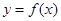 的过原点的切线方程.
的过原点的切线方程.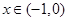 ,恒有
,恒有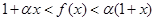 .
.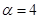 时,求最大实数
时,求最大实数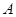 ,使不等式
,使不等式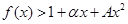 对
对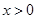 恒成立.
恒成立.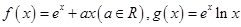 (e为自然对数的底数).
(e为自然对数的底数).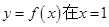 处的切线为
处的切线为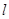 ,若
,若 ,求a的值;
,求a的值;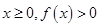 恒成立,试确定
恒成立,试确定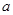 的取值范围;
的取值范围; 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.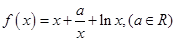 ,
,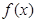 有最值,求实数
有最值,求实数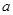 的取值范围;
的取值范围;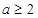 时,若存在
时,若存在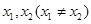 ,使得曲线
,使得曲线 在
在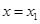 与
与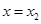 处的切线互相平行,求证
处的切线互相平行,求证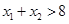 。
。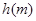 与起跳后的时间
与起跳后的时间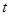
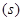 存在函数关系
存在函数关系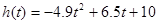 ,则瞬时速度为0
,则瞬时速度为0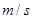 的时刻是( )
的时刻是( )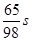
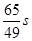
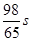
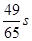
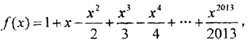 设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b
设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b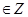 ) 内,,则x2+y2=b-a的面积的最小值为( )
) 内,,则x2+y2=b-a的面积的最小值为( )
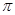
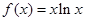 ,若
,若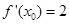 ,则
,则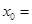 ( )
( )