题目内容
【题目】等比数列{an}的各项均为正数,且a2=2,a4=![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an , 求数列{bn}的前n项和Tn .
【答案】
解:(Ⅰ)设数列an的公比为q,则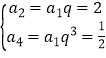
解得q=![]() ,a1=4(负值舍去).
,a1=4(负值舍去).
所以![]() .
.
(Ⅱ)因为![]() ,bn=log2an ,
,bn=log2an ,
所以![]() ,…(8分)bn﹣bn﹣1=(﹣n+3)﹣[﹣(n﹣1)+3]=﹣1,
,…(8分)bn﹣bn﹣1=(﹣n+3)﹣[﹣(n﹣1)+3]=﹣1,
因此数列{bn}是首项为2,公差为﹣1的等差数列,
所以![]()
【解析】(Ⅰ)由a2=2,a4=![]() , 利用等比数列的通项公式得
, 利用等比数列的通项公式得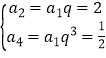 , 解得q=
, 解得q=![]() ,a1=4,由此能求出数列{an}的通项公式.
,a1=4,由此能求出数列{an}的通项公式.
(Ⅱ)因为![]() , bn=log2an , 所以
, bn=log2an , 所以![]() , 由此能求出数列{bn}的前n项和Tn .
, 由此能求出数列{bn}的前n项和Tn .
【考点精析】根据题目的已知条件,利用等比数列的通项公式(及其变式)和数列的前n项和的相关知识可以得到问题的答案,需要掌握通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系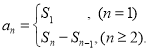 .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立y关于t的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
【题目】某产品的广告支出x(单位:万元)与销售收入y(单位:万元)之间有下表所对应的数据:
广告支出x(单位:万元) | 1 | 2 | 3 | 4 |
销售收入y(单位:万元) | 12 | 28 | 42 | 56 |
(1)画出表中数据的散点图;
(2)求出y对x的回归直线方程![]() ;
;
(3)若广告费为9万元,则销售收入约为多少万元?
参考公式: