题目内容
【题目】某市一个社区微信群“步行者”有成员100人,其中男性70人,女性30人,现统计他们平均每天步行的时间,得到频率分布直方图,如图所示:

若规定平均每天步行时间不少于2小时的成员为“步行健将”,低于2小时的成员为“非步行健将”.已知“步行健将”中女性占![]() .
.
(1)填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘步行健将’与性别有关”;
列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘步行健将’与性别有关”;

(2)现从“步行健将”中随机选派2人参加全市业余步行比赛,求2人中男性的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:![]() ,其中
,其中![]() .
.

【答案】(1)见解析;(2)见解析
【解析】分析:(1)根据直方图完成列联表,利用公式![]() 求得
求得![]() ,与邻界值比较,即可得到结论;(2)
,与邻界值比较,即可得到结论;(2)![]() 的可能取值为
的可能取值为![]() ,利用组合知识根据古典概型概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得
,利用组合知识根据古典概型概率公式求出各随机变量对应的概率,从而可得分布列,进而利用期望公式可得![]() 的数学期望.
的数学期望.
详解:(1)据频率分布直方图,“步行健将”的人数为![]() ,
,
其中女性有7人,填写表格如下:
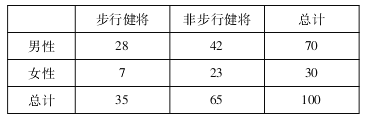
故![]()
故在犯错误的概率不超过0.05的前提下不能认为“是否为‘步行健将’与性别有关”.
(2)依题意知![]() 的可能取值为0,1,2,所以
的可能取值为0,1,2,所以
![]()
分布列为
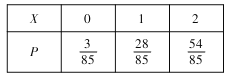
故![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的![]() 班和文史类专业的
班和文史类专业的![]() 班各抽取
班各抽取![]() 名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
优秀 | 非优秀 | 总计 | |
| 14 | 6 | 20 |
| 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
附:参考公式及数据:
(1)统计量:![]() ,(
,(![]() ).
).
(2)独立性检验的临界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
则下列说法正确的是
A. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
B. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关
C. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
D. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关