题目内容
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立y关于t的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
【答案】(1)y=0.16t+6.44.(2)7.72万吨.
【解析】
(1)利用最小二乘法求出线性回归方程的系数![]() ,即可得到其线性回归方程.
,即可得到其线性回归方程.
(2)2019年对应的![]() 为
为![]() ,将
,将![]() 代入回归方程即可求出预测值.
代入回归方程即可求出预测值.
解(1)由题意可知:![]() =
=![]() (1+2+3+4+5+6)=3.5,
(1+2+3+4+5+6)=3.5,![]() =
=![]() (6.6+6.7+7+7.1+7.2+7.4)=7,
(6.6+6.7+7+7.1+7.2+7.4)=7,
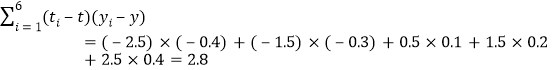 ;
;
![]() =2.52+1.52+0.52+0.52+1.52+2.52=17.5,
=2.52+1.52+0.52+0.52+1.52+2.52=17.5,
则![]() ,又
,又![]() ,
,
所以y关于t的线性回归方程为![]() .
.
(2)由(1)可得,当年份为2019年时,年份代码![]() ,
,
此时![]() ,
,
所以可预测2019年该地区该农产品的年产量约为7.72万吨.

练习册系列答案
相关题目
【题目】在一块耕地上种植一种作物,每季种植成本为1000元,此作物的市场价格和这块地上的产量均具有随机性,且互不影响,其具体情况如下表:
作物产量(kg) | 300 | 500 |
概率 | 0.5 | 0.5 |
作物市场价格(元/kg) | 6 | 10 |
概率 | 0.4 | 0.6 |
(1)设X表示在这块地上种植1季此作物的利润,求X的分布列;
(2)若在这块地上连续3季种植此作物,求这3季中至少有2季的利润不少于2000元的概率.
