题目内容
9.{an}是各项均为正数的等比数列,已a1=2,a3=8.(Ⅰ)求数{an}的通项公式;
(Ⅱ)求数{log2an}的前n项和Tn.
分析 (I)利用等比数列的通项公式即可得出;
(Ⅱ)由(Ⅰ)得log2an=$lo{g}_{2}{2}^{n}$=n.利用等差数列的前n项和公式即可得出.
解答 解:(Ⅰ)设等比数列{an}的公比为q>0,
∵a1=2,a3=8.
∴8=2q2,解得q=2.
∴an=2n.
(Ⅱ)由(Ⅰ)得log2an=$lo{g}_{2}{2}^{n}$=n.
∴数{log2an}的前n项和Tn=1+2+3+…+n=$\frac{n(n+1)}{2}$.
点评 本题考查了等比数列的通项公式、对数的运算性质、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.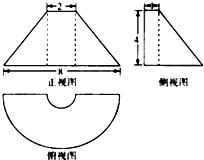 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
 如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )
如图是某几何体的三视图,正视图是等腰梯形,俯视图中的曲线是两个同心的半圆组成的半圆环,侧视图是直角梯形,则该几何体的体积等于( )| A. | 12π | B. | 16π | C. | 20π | D. | 24π |
14.执行右面的程序框图,若输入x=7,y=6,则输出的有数对为( )
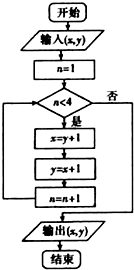

| A. | (11,12) | B. | (12,13) | C. | (13,14) | D. | (13,12) |
1.设a∈R,且(a-i)•2i(i为虚数单位)为正实数,则a等于( )
| A. | 1 | B. | 0 | C. | -1 | D. | 0或-1 |
 根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015
根据下列算法语句,将输出的A值依次记为a1,a2,…,an,…,a2015